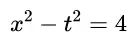分类： 生活

如果我们将两个 4G 内存插入内存插槽，得到的内存地址空间是 0 到 8G 吗？是不是 0 到 4G 是第一根内存，4 到 8G 是第二根内存呢？实际情况相差甚远，内存在物理地址空间的映射是分散的。一部分原因是 4G 以下有 Memory map IO（mmio）空间和 PCIe 的配置空间，另一个原因是 Interleaving 会打撒内存地址到各个 Channel、DIMM 甚至是 Rank 和 bank 上。今天我们就一起来了解一下 x86 系统的地址空间分布。

物理地址空间

一个典型的物理地址空间是这样的：

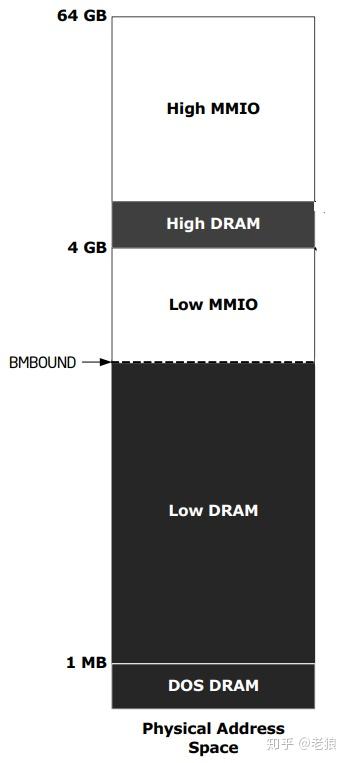
其中只有灰色部分是真正的内存，其余都是 MMIO。而内存被分为 High DRAM 和 Low DRAM，如图：

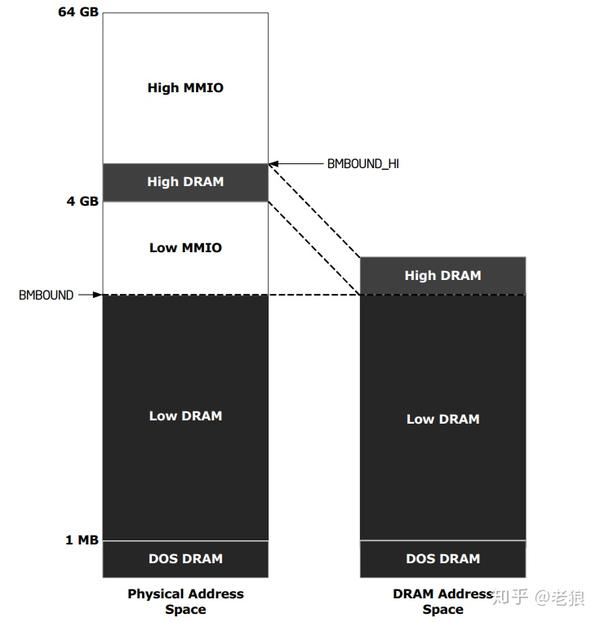
为什么要把内存强行分割成两块呢？因为历史的包袱。最早内存都很小，32 位的地址（4G）空间看起来永远也用不完，低地址被分配给内存用，高地址就自然而然被分配用来给 Memory map IO。既然已经分给它们了，为了兼容以前的驱动，这一块就被固定下来。再有内存就只能从 4G 以上分配了。

Low MMIO 和 High MMIO

Low MMIO 结构如下图：

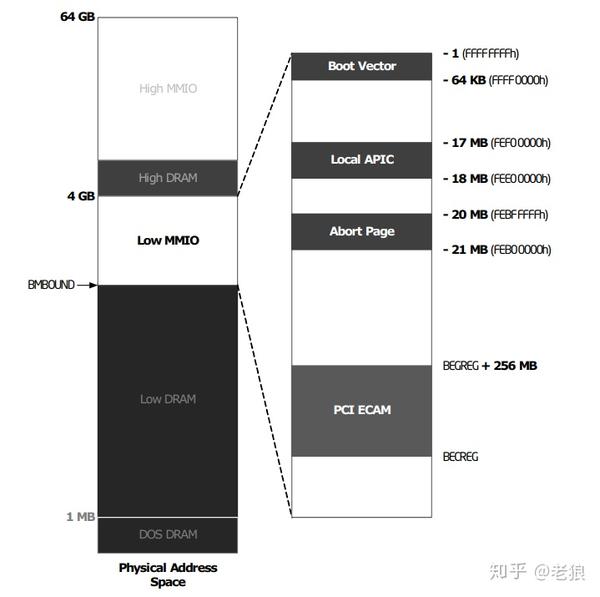
其中有几块要特别说明一下：

1.Boot Vector 的空间是 BIOS 内容映射的地址，它的大小是可以调节的，为了满足不同大小的 BIOS。

2.Local APIC 是 APIC 中断模式各个内核 local APIC 寄存器的映射地址。APIC 的中断可以参考这篇文章：

老狼：计算机中断体系二：中断处理

３.PCI ECAM 也有叫做 PCIBAR，是 PCIe 配置地址空间的映射地址。它的起始地址可调，台式机 BIOS 一般会把它设置得很高，这样 4G 以下内存会比较大，方便 32 位 Windows 使用。举个例子，如果我们把 PCIe BAR（BEGREG）设为 0x80000000，那么尽管插了 8G DIMM，4G 以下也不会超过 2G 的内存可以使用，而 2 到 8G 的真实内存都被映射到在 4G 地址空间以上了，而这些是 32 位 Windows 使用不了的。所以有的主板运行 32 位操作系统发现可用内存小了一大块就是这个原因。它的大小可以修改，一般可以设为 64MB 和 128MB。PCIe 的详细内容可以参考这篇文章：

老狼：深入 PCI 与 PCIe 之二：软件篇

High MMIO 被 BIOS 保留作为 64 位 mmio 分配之用，例如 PCIe 的 64 位 BAR 等。

Low DRAM 和 High DRAM

4G 以下内存最高地址叫做 BMBOUND，也有叫做 Top of Low Usable DRAM (TOLUD) 。BIOS 也并不是把这些都报告给操作系统，而是要在里面划分出一部分给核显、ME 和 SMM 等功能：

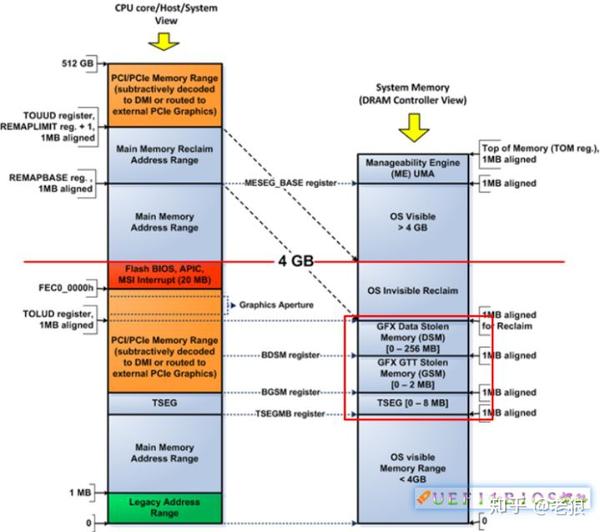
4G 以上的内存最高端叫做 Top of Up Usable DRAM (TOUUD) ，再上面就是 High MMIO 了。

1MB 以下比较特殊，里面全部都是已经被淘汰的传统 BIOS 和 DOS 关心的内容，我们叫它 DOS Space 或者 Legacy Region：

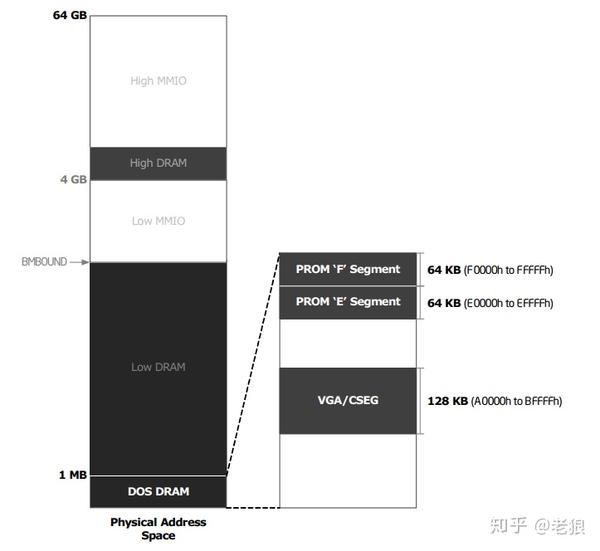
在那里，我们习惯用传统的实模式地址来划分它们的具体内容：

1.0~640KB，传统 DOS 空间。

2.A 段和 B 段，传统 SMM 空间。VGA 的 MMIO 也被映射到这里，可以通过寄存器切换。

3.C 段和 D 段，legacy opROM 映射空间和 EBDA 空间。

4.E 段和 F 段，BIOS 空间的 Lower 和 Upper 映射地址。BIOS 的 rom 内容也会被映射到这里，方便 Legacy BIOS 实模式跳转到保护模式。

内存的 Interleave

从前面可以看出内存在地址空间上被拆分成两块：Low DRAM 和 High DRAM。那么在每块地址空间上分配连续吗？现代内存系统在引入多通道后，为了规避数据的局部性（这也是 Cache 为什么起作用的原因）对多通道性能的影响，BIOS 基本缺省全部开启了 Interleaving，过去美好的 DIMM 0 和 DIMM 1 挨个连续分配的日子一去不复返了。

什么是 Interleaving？简单来说，就是让内存交错起来，如下面的动图：

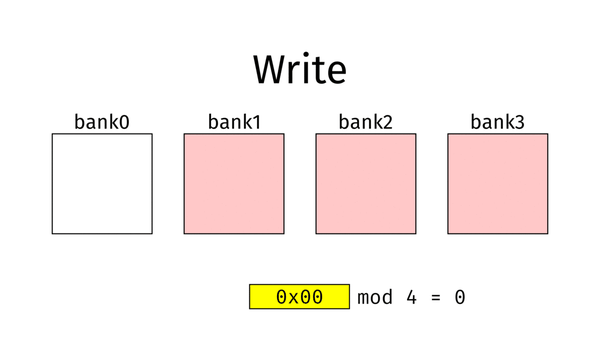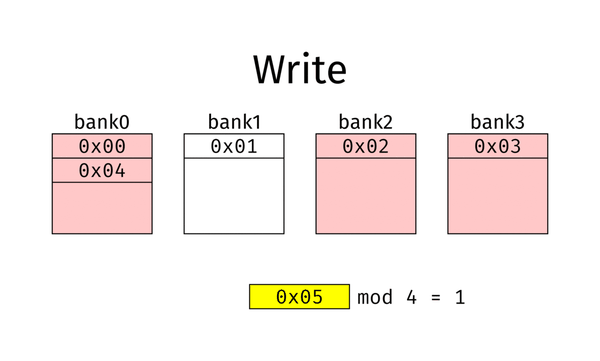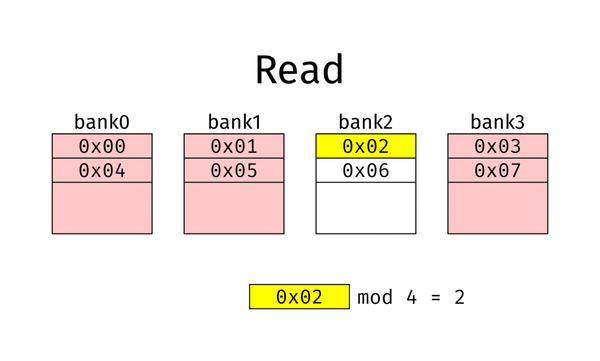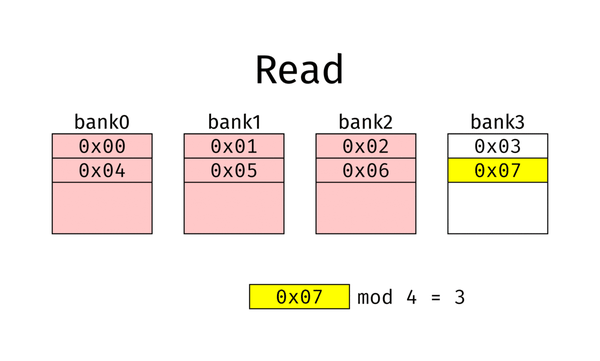
这是一个 bank 层级的模 4 的 interleaving。在桌面电脑上，常见的还有 Channel 级的、DIMM 级的和 Rank 级的。Channel/DIMM/Rank/bank 这些概念可以参考这两篇文章：

老狼：内存系列一：快速读懂内存条标签老狼：内存系列二：深入理解硬件原理

服务器上 Interleaving 更是不可或缺，它的粒度更细，可以达到数十 bytes 层级的 interleave，它和内存的其他特性，如类似磁盘阵列 RAID 的内存 spare, mirror 特性，构成了复杂异常的内存映射系统。在 BIOS 里面，台式机 / 笔记本内存映射相对简单，只有一个大表和数十个寄存器；而在服务器 BIOS 中，有数个相互关联的大表和寄存器阵列来解码（decode）内存的请求，代码的硬件逻辑也是相当复杂。关于它，我会有一篇专栏文章讨论地址译码和地址反向解码，详细内容那里再说，这里只需要知道，物理内存分布在各个 DIMM 上就够了。

物理地址到内存单元的反推

BIOS 实际上一手导演的内存的分配，它当然可以从任何物理地址反推回内存的单元地址。我们可以用下面一组数据来唯一确定某个内存单元：

Channel #;DIMM #; Rank #;Bank #;Row #;Column #

在内存分配表缺失的情况下，BIOS 甚至可以通过它填过的寄存器重建这个映射表。但实际上 BIOS 并不希望一般用户知道这些信息，因为有安全性问题。

暴露内存信息容易招来内存侧信道攻击（Side Channel），比较有名的有 Row hammer 攻击。简单的来说它是通过反复写某个内存单元，借助内存的特性，希望影响相邻 Row/Column 的内容。详细内容可以参考这里：

老狼：内存不刷新会怎样？内存的物理攻击和旁路攻击

有些情况确实需要知道这些信息，就是内存出错的时候。和大家想象的不同，内存是会出错的。尤其云服务器中内存的出错是十分频繁的。出错起来也千奇百怪，开始可能是偶尔的随机错误，经过 ECC 等校正后，就再也不会复现；而有时是某个 Bit 总是出错，进而慢慢的整个 row、column 或者相邻的 cell 开始出错，从可以纠正的错误变成不可修正的错误，导致服务器必须停机。这时候就必须知道哪个内存坏了，进而换掉它。BIOS 的报错是通过 WHEA:

老狼：WHEA 原理和架构

报告给操作系统，但这个信息里面只有物理地址，如何才能知道是哪个内存单元坏了呢？在 Linux 上面可以通过 edca(参考资料 4)，有编程经验的同学可以通过 edca 的程序接口（参考资料 3），可以得到更加丰富的信息。

如何关掉 Interleaving

对内存有特殊需求的朋友，如果希望内存连续，可以在 BIOS 里面关闭所有的Interleaving 来达成这个目标：

注意是所有的。之后可以通过 SMBIOS 来看到内存分布信息（dmidecode）。

结论

BIOS 作为内存的大管家，也负责内存的分配和映射 memory map。它会把这些信息通过 E820, GetMemoryMap 函数和 SMBIOS 传递给操作系统。操作系统在此基础上再建立页表，产生虚拟地址。

另一篇相关的文章:

老狼：神秘消失的内存去哪了？

BIOS 培训云课堂：

卓易云课堂

参考资料：

实际上从天体物理和核物理的角度上来说，不太可能出现同时缺少铁和碳元素的星球，除非它是一个第三星族恒星……

然后说正题，人类广泛使用铁基金属一方面是因为铁本身相对易于获得，炼铁所需的工艺水平相当之低。但我个人的看法是铁本身的独特属性可能更为重要。

在系统学习金属材料的时候就会发现铁是一个非常独特的金属。可以具体列出这么几个：

1. 铁作为一个室温为体心立方结构的金属，其室温韧性居然出奇的好。从金属结构上来说，体心立方金属的韧性应该相对较差一点，典型的例子就是 Cr、W 这些金属。当然，铁也不是唯一有这个特点的，比如另一个过渡金属钒，也是体心立方结构，也具有很好的室温韧性。
2. 作为一个体心立方金属，铁的韧脆转变温度低于常见温度（除非去南极，一般碰不上）。这点钨等金属哭晕在厕所。另一个是钒，钒具有更低的韧脆转变温度，但是……
3. 铁有一个重要的面心立方（奥氏体）/ 体心立方（铁素体）相变。像这种在接近单质态时具有最密堆积到次密堆积形式的一级相变的金属是很少的，尤其是相变前后的力学性能都还很不错。由于中间多了一个相变且其奥氏体和铁素体的碳溶解度有一定差异，就为热处理赋予了极大的自由度。所以有的老师会说天下钢铁工艺一旦，热处理独占七斗的说法。实际上几乎没有任何一种材料的热处理工艺能有钢铁这么丰富。
4. 铁的面心立方（奥氏体）/ 体心立方（铁素体）相变受化学成分影响大。如果需要的化可以做出超大范围的改变，甚至得到不会发生相变的奥氏体或者铁素体钢。所以从极低温到高温都有铁的身影……另一个相似的金属是钛，但是很可惜没有铁的两相互补性强。
5. 铁对杂质元素很不敏感，基本是最粗糙的元素之一，杂质多了性能会下降，但不会直接死给你看。相比之下，钒这家伙尽管室温韧性很好，但是杂质一多就分分钟碎给你看。
6. 奥氏体几乎没有磁性，而铁素体还有一个铁磁 / 顺磁转变。所以铁能在磁性上玩很多花活。
7. 铁还有一个神奇的亚稳的面心立方（奥氏体）/ 体心四方（马氏体）相变。这种亚稳态的相变与其中固溶的碳有显著关系，导致铁碳合金体系可以轻易实现过饱和固溶体并同时降低晶体对称性。巧就巧在这个晶体对称性的降低没有那么多，马氏体仍然可以近似看做是体心立方结构，（参考 1）这家伙在剧烈强化（过饱和固溶、快冷缺陷多等）的同时居然韧性还可以。钛合金也有类似性质，但是效果不如铁（钛合金的马氏体太弱了）。
8. 铁的化学性质不那么活泼，冶炼铁不需要高端技术，完全可以依靠化学过程进行。作为对比凡是能和铁一战的金属，没有一个是好冶炼的（比如钛），凡是比铁好冶炼的，力学性能上都能被钢铁秒成渣渣（比如铜）。
9. 更神奇的事铁这家伙室温性能不错的同时，高温性能居然也可以。
10. 铁能自发的形成氧化膜。注意这点和中学课本不一样，铁是可以自发形成氧化膜的（不是铁锈，是氧化膜）。但是铁的氧化膜保护作用不强，因为氧化铁中氧扩散较强。但是神奇的部分来了，铁作为金属和重要的耐蚀元素（Cr 或者 Al）都是固溶的，但是铁的氧化物，他与耐蚀元素的氧化物基本都是不怎么固溶的。所以，他不会破坏耐蚀元素形成的保护层。所以这家伙的耐蚀性居然可以很好……
11. 铁的密度相当合理。其实几乎在任何场合，铁的密度都不至于太差。虽然相比轻金属大点，但是也没大到完全不可接受。实际上如果铁具有铜的密度（8.9），马斯克就得考虑考虑能不能造不锈钢火箭了。
12. 实际上从材料结构上来考虑，铁是很特殊的。晶体缺陷的研究表明铁素体中的缺陷聚集形态和多数体心立方金属都不一样，比如特立独行的 100 型位错环。另一个特立独行的是钒，这家伙顶着体心立方金属的名头，变形的时候却像面心立方金属那样很容易出孪晶。

还有一些特点是他的主要合金元素碳赋予的，铁碳合金实际上并不那么好操控，这也是为什么钢比铸铁晚那么多才出现的原因。但是好就好在，即使不那么理想的铸铁，性能依然相当可以：

1. 碳是小原子，在铁中的扩散速度快，相对容易实现均匀化。这点秒杀无数合金，很多铜合金动不动就要好几天的均匀化热处理。同时也意味着可以比较容易得对铁碳合金脱碳和增碳。
2. 铁的碳化物没有那么稳定，所以铸铁缓慢冷却时可以得到铁碳固溶体 + 石墨的组织。避免了产生大量碳化物导致的硬脆。也赋予了通过热处理或者添加其他元素形成或者消除碳化物的能力。
3. 上一条导致了铁碳合金体系的一个特色，就是这家伙是 2 个元素的三相平衡，实际上铁碳平衡是由铁 – 石墨和铁 – 渗碳体两个平衡体系共同建立的。即使是在铸铁中都能给你玩出花来。
4. 石墨这个东西尽管会破坏铁的力学性能，但是这家伙导热极好，能缓解热应力。
5. 还是石墨这个家伙，当铁水冷却时石墨析出，这个过程体积的膨胀的。而我们都知道热胀冷缩，所以石墨的析出恰好一定程度上对消掉了凝固收缩。这能让其他合金体系羡慕死。
6. 石墨具有六方晶系的结构，拥有两个特殊的生长方向（a 方向：六边形方向，c 方向：垂直六边形方向）。这导致通过改变石墨生长方向可以赋予石墨不同的形态，于是就有了力学性能较差但是减震、传热和冶炼容易得灰铸铁，以及力学性能很好的球墨铸铁（某些性能堪比碳钢）。

对着元素周期表翻一遍，基本上找不出第二个元素能把这么多特点集合到一起。这也是为什么现在的金属材料体系分为钢铁材料和非铁材料（有色合金）两大块的原因。

另外，所有钢铁之外的金属材料加起来，使用量都远低于钢铁。所以通常分类是：铁、钢、有色合金。实际上几乎所有金属结构材料都能找到他的钢铁替代品（一般性能要差）。比如高温合金的替代品（耐热钢和铁基高温合金）、轻合金的替代品（轻质钢）等等。

哦对，人类到目前为止有且仅有一种材料的使用规模可以与钢铁相比，就是水泥。

所以曾经有这么一个段子，如果评选人类最重要的材料的话，钢铁和水泥花落谁家不好说，但是如果选两个的话，绝对找不出第三个候选……

应评论区要求继续更一下：

继续说一下铁，关于铁的冶炼。其实铁的另一个特点就是铁碳相图在碳含量为 4.3%左右时有一个共晶相变，相变温度只有 1148 度。这一温度甚至比纯铜的熔点都高不了多少。所以，熔炼铸铁非常容易。

而铁和碳这个组合我们前面已经说了，扩散是很快的。大家不要被固态扩散给吓到，相比于有色合金中的扩散，铁中的碳扩散可以说是飞速了（作为对比，氢扩散就可以说是光速了）。这就导致我们无论是给熟铁（近似认为是纯铁）加碳还是给生铁脱碳都相对容易。

这就让人类在获得熔炼钢的高温之前，就能获得钢。比如在凡尔纳创作的《神秘岛》中就介绍了两种主要的制造钢铁的思路：海绵铁锻打加碳和生铁脱碳。前者就是我们的老祖宗最开始的炼钢工艺，后者其实在网上更有名，大名鼎鼎的大马士革钢就是用这种原理生产的。这种方法的基本工艺是把生铁和高碳的铸铁或者高碳钢混合起来，或者用脱碳剂把（比如铁矿石）高碳铁包裹起来，然后锻打，实现脱碳。

（这个和锻造是不一样的，脱碳是主要目的，每次变形量很小，所以不容易开裂。当然了，当时也做不到大变形）

这种工艺在别的合金体系简直是不可想象的

而实际上还有一个其他合金体系羡慕死的特性：钢铁的主合金元素是碳，炼铁的燃料是什么？还是碳。炼铁的时候什么东西还原的氧化铁，一氧化碳。铁水也好，铸铁也好，脱碳用的是什么？氧（氧化物或者直接是氧气），焦炭燃烧用的是什么？氧！整套冶炼过程，无论是加热还是调节成分还是保护气氛，全在铁、碳、氧里面解决了。这简直梦寐以求好不好。

然后应邀更一下别的金属体系。先说人类文明的第一代金属材料：铜，我们大致上与铁对应的看。

1. 铜是一个非常忠诚的面心立方结构金属，从室温到融化，坚定的站在面心立方这一面，与两面三刀的铁还有身在曹营的钒都不一样。面心立方的金属有个特点，就是非常容易变形，塑性和韧性极好，但是代价是强度不高、刚度不足。比如典型的金、银、铝都是这样的。实际上铜在常见面心立方金属中算是强度高的那一部分了，像金银这种货色都不配合铜比。所以铜非常容易进行压力加工、非常容易冲压。
2. 面心立方赋予铜的另一个特点是铜中的位错非常容易产生但是也非常容易被消除。所以铜不适合工作在高温之下。即使进行过锻造的铜，也很容易在高温下回复从而造成性能崩溃。这导致铜合金的软化温度相对比较低，我们目前常见的铜合金通常都只能长时间用在 300 度或更低。（钢铁看了斜眼，铝合金看了泪目）
3. 面心立方结构没有韧脆转变，所以不同担心它突然变脆了。
4. 目前常见的铜合金体系基本都是面心立方的，没有相变，导致热处理手段很单一。实际上我们是可以给铜添加合金元素让他具有一个马氏体相变的，这玩意也有成果，比如铜基形状记忆合金。但是问题在于…..铜合金的马氏体相变相比钢性能上差很远，而且热处理工艺很费时。但是形状记忆是个好特性，不过铜基的转变温度一般很低（远低于 0 度的那种低）
5. 铜的密度达到了 8.9，比铁高 12%，这个密度怎么说呢。说高不高，说低不低，就比较拧巴。尤其是高强度的铜合金实际上很难做到，所以他的比强度实际上太差。这点严重的限制了铜合金的用途。
6. 如果不考虑矿的话，铜的冶炼非常容易！还原铜比还原铁容易的多。
7. 所有的有色合金基本都有一个通病，就是没有明显的主要合金元素。作为对比，钢铁里主要合金元素不用看都是碳，哪怕是超低碳不锈钢里碳已经很少很少了，但你看名字就知道碳肯定有巨大的影响。而铜不行，目前铜的合金体系可以简单归类为 Cu-Al、Cu-Zn、Cu-Sn 及其变种合金。（伪合金我们就不讨论了）而这类合金都有一个问题，就是都有明显的优缺点，而缺点难以改进。
8. 青铜（Cu-Sn 合金）是人类第一种能规模化冶炼的合金，从化学角度上来说青铜的耐海水、蒸汽和碱性溶液的腐蚀性非常优秀，但是从材料学角度来说青铜的力学和冶金性能稀烂无比，强度太低、铸造性太差，动不动就 Sn 偏析，一个不小心就需要热处理几十个小时进行均匀化（这在钢铁中是不可想象的）。
9. 铝青铜（Cu-Al 合金）的性能要比青铜好，但是铝这个元素是个坑，冶炼太过困难。而且即使放弃冶炼困难的问题，铝青铜还有一个要命的缺陷“自动退火脆性”。Cu-Al 合金在 565 度左右（Al 11.8%）有一个相变，会形成一种脆性的 CuAl 金属间化合物。这个缺点并非不能解决，但是需要对成分和工艺都进行更好的控制（而且会引入对碳的敏感性）。另外说一句，高端船用螺旋桨一般就是 Cu-Al 合金系的，说明这个合金还是有他的优势的。而 Al 这个元素还有巨坑，就是熔炼的时候这家伙极易吸氧形成固体夹杂……那简直是冶金工程师的噩梦了……
10. 黄铜（Cu-Zn 合金）外观漂亮、铸造简单、性能还也凑合。但是问题在于这家伙不能做热处理强化啊……工艺呆板了好多好多，性能自由度也低了很多。

所以铜比较尴尬的是作为结构材料，他的许多许多特性都很出色，但同时都有缺点难以克服。比如强度不高……说白了几乎所有的铜合金都死于强度不高。冶金学家是真的拿铜合金的强化没什么办法，你想啊一个强度到 400-500MPa 的铜都能称自己为高强度铜，一个强度 1GPa 的钢敢说自己是高强度钢吗（高强度钢的定义一般是是屈服强度＞1180MPa）

尽管铜的力学性能不能和钢媲美，但是铜在铁器时代并不是没有竞争力的。相比铸铁铜有两个有点，或者说是铸铁的缺点：

1. 铜抗拉又抗压，而铸铁，尤其是灰铸铁不抗拉。原因是灰铸铁中出现的石墨切割了组织，导致额外的应力集中，所以灰铸铁面对拉应力的时候要打折扣；
2. 铜的断裂韧性非常好，而铸铁的韧性不大行。尤其是抗冲击性能，铸铁远远逊色于铜，这事一直到球墨铸铁被发明才得到改善，导钢铁时代才完全解决。

所以古代铸造火炮的时候（古代的工艺下，火炮只能铸造），铜炮在一定程度上是优于铁炮的。但是古代铜合金的制备也远远不能和现在相比，所以铸造的火炮炸膛是家常便饭……即使是“天才”乌尔班本人死于火炮炸膛……

再简单说一下使用量最大的有色合金——铝：

1. 铝的最大的缺点就是冶炼困难。电解铝没有大规模的电力基础想都不要想……
2. 铝合金的高温性能非常差。毕竟对一个熔点只有 600 来度的家伙，不能期望他有很好的高温性能。所以但凡温度高点，比如 300 度，就不敢用铝。（高温铝合金一般也就用 200 左右温度）
3. 铝合金的密度非常低。无与伦比的低（只有镁合金可以一战，但是……镁合金的性能……），这导致室温下铝合金的比强度其实还挺乐观。
4. 铝也是面心立方结构，但是这个面心立方和铜还有点不一样。铝合金不容易形成孪晶（层错能很高），容易形成位错。当然，这也意味着铝很多性能接近铜，在高温下一样都是菜鸡。
5. 最常用的铝合金体系是 Al-Si 合金，但是这货他严格来说是个伪合金……如果不是有变质工艺，Al-Si 合金根本就做不出来，而变质工艺依赖的 NaF、P 之类的……又得别的工业提供
6. 几乎所有的 Al-Si 之外的铝合金体系都严重偏离共晶点，说人话就是铸造性能稀烂（相比于铸铁）。（Fe-C 系共晶点 4.3%，Al-Si 是 12.6%，Al-Cu 系是 33.2%，Al-Mg 是 35%…….没法看，完全没法看）
7. 热处理工艺非常单一，其实铝合金常用的热处理基本就是时效、退火、固溶……手段单一，所以无法大幅度调节性能。

其实，铝合金和钛合金有很多相似的地方，都是在冶炼上吃亏……

当然，其实还有一个很多有色合金有的巨大问题，就是怎么连接。钢的可焊性其实相当不错（特种钢除外），但是有色合金的连接说多了都是泪啊……

当年臭鼬工厂为了搞钛合金的加工和连接，基本全部重新设计了全套的加工工艺……

实际上对比有色合金体系就会发现，有色合金中的合金元素基本都是代位原子，而铁中最重要的碳他是间隙原子，二者的扩散能力上有天壤之别。这也是像镍和钴这样的金属不能替换铁的原因

而且钢铁材料里加的合金元素真是少啊……碳他是真的给力啊……

最后从性能上总结来说，铁他是一个低配的六边形战士……样样都不是最好的，但是面板都有 80 分，加几个技能点就到 90+ 了。能输出能打野能肉盾能推塔能辅助

而其他大多数合金基本都是偏科战士……个别属性超过 100，但是某一方面太拉胯，基本就是个 50 分水平。技能点狂点也就加到及格线，打得了输出就打不了辅助……

我去年没事干干过这个, 计算字体聚类.

㬺幐(U+3B3A, U+5E50)
墫壿(U+58AB, U+58FF)
鬬鬭(U+9B2C, U+9B2D)
晚晩(U+665A, U+6669)
凉凉(U+51C9, U+F979) 我以后也要用这个词.

先随手创建一个文件夹, 然后新建一个 notebook.

选择 CJK 区 “㐀(U+3400)” 到” 龥(U+9FA5)”共 27558 个字.

有汉字有繁体字, 可能有异体字, 这个范围应该没有日语字…

字号 25 号, 字体使用混合字体 YaHei Consolas Hybrid, 对中文来说就是微软雅黑

all=StringPartition[FromCharacterCode[Range@@ToCharacterCode["㐀龥"]],1];
toImg=Rasterize@Style[#,FontSize->25,FontFamily->"YaHei Consolas Hybrid"]&;

然后用异步渲染把字都渲染出来.

并行策略选择了 Coarsest Grained, 适用于每个单元执行时间相近的情况.

虽然我也不知道并行快还是不并行快……

但是这样写就算内核突然崩溃了下次不用从头跑, 比较安全…

$now=Now
$here=DirectoryName@NotebookFileName[];
Exporter[num_]:=Block[
  {name=$here<>ToString@num<>".png"},
  If[FileExistsQ@name,Return[]];
  Export[name,toImg@FromCharacterCode[num]]
];
ParallelMap[Exporter,Range@@ToCharacterCode["㐀龥"],Method->"CoarsestGrained"];
Now - $now

然后去上课, 上完课回来肯定就好了

渲染完洗一下内存, 再全部读进来, 关了重开也行…

然后随手选个聚类算法呗, 参数靠魔法…

瞎算了几次, 发现一个比较稳的方法.

可以分批次训练, 每批 2000 个字,聚类半径设为 10.

一起跑实在太慢了, 然后考虑到制字表的时候也是相似的字放在一起的, 应该不会出现大问题…

或者可以用快速聚类, 大约 1 分钟, 进行一个初步的空白区域大小划分.

然后再细致的对划分二次聚类, 毕竟聚类这个复杂度是超线性的, 划分一下虽然要算多算一次, 但还是有加速效果的…

$now=Now
$here=DirectoryName@NotebookFileName[];
all=Association[#->Import[#]&/@FileNames["*.png",$here]];
pat=Select[FindClusters[all,
 Method->{"NeighborhoodContraction","NeighborhoodRadius"->10}],
Length@#>1&];
try1=Select[FindClusters[Association[#],
 Method->{"NeighborhoodContraction","NeighborhoodRadius"->10}],
Length@#>1&]&/@Map[#->all[#]&,pat,{2}];
DeleteDuplicates/@Map[all,Flatten[try1,1],{2}]
Now-$now

然后去上另一节课, 上完差不多就能出图了, like this!

效果不够好, 基本上都是偏旁不同, 那就三次聚类呗, 现在已经只有 1690 个字了….

try2 = Select[
  FindClusters[Association[Map[# -> all[#] &, Flatten[try1]]],
    Method -> {"NeighborhoodContraction", "NeighborhoodRadius" -> 4}],
  Length@# > 1 &]; Map[all, try2, {2}]

缺字会被垒到一起, 很迷, 还有就是异体字太多

我本来是想用机械智障造字….

构造一个 GAN, 生产者生产随机像素, 监督者来判别这个字存不存在…

然而…好像效果不咋的, 都没法通过我这个人的图灵测试, 毕竟…….

有噪点的都是新造的字啊….GG

更新：这篇文章已经被我的第 2 本书《什么是相对论（狭义篇）》（长尾科普系列丛书 -02）收录，觉得在手机上看不太方便，或者想让自己和朋友家的中小学生也看看的，不妨看看对应的纸质书籍：

1905 年，爱因斯坦正式提出了狭义相对论；1908 年，闵可夫斯基给出了狭义相对论的几何表述，也就是我们这里说的闵氏几何。爱因斯坦一开始对这套几何语言很反感，认为这些纯数学上的“花架子”没什么用，还增加了相对论的复杂度。但是，他很快就发现闵氏几何非常重要，发现这绝不是什么纯数学技巧，而是有着深刻物理内涵的洞见。而且，如果要建立广义相对论，少了它根本不行。

几何语言清晰直观，在处理许多问题时有很大的优势，这在双生子佯谬里体现得非常明显：使用代数语言，使用洛伦兹变换去处理双生子佯谬，其中难度之大思维之绕，绝对是对智商极大的考验；而使用几何语言，这个问题就简单得不像是个问题。然而，目前绝大部分介绍相对论的书籍文章还是使用的代数语言，所以你还是能经常看到许多人在一些非常简单的问题上纠缠不清，争论不休。

梁灿彬老师说他上世纪 80 年代从“言必称几何”的芝加哥大学回来以后，就一直在国内大力推广相对论的几何语言，但是不明白为啥过了三十多年大众对它还是很排斥。长尾科技就在这篇文章里跟大家好好聊一聊，希望能够解开大家跟闵氏几何之间的心结。

因为这是从零开始的一篇文章，所以我暂时就只谈相对论里最简单的几何语言，也就是狭义相对论里的闵氏几何。至于广义相对论里涉及的黎曼几何，我们后面再说。

01 为什么很多人觉得几何语言难？

了解相对论的人大多知道一点闵氏几何，知道我们可以通过画时空图的方式来解决一些很复杂的问题，但是他会觉得闵氏几何很难：把时空图画出来很难，画出来之后去解释时空图更难。当看到别人对着时空图“轻而易举”地把问题解决了，他心里没底。他无法理解为什么你说时空图里的这个代表了相对论的里的那个，为什么你对时空图里的一些点、线、面做这样的处理就对应着相对论里的那个问题。所以，他觉得你在时空图里做的那些几何操作非常“虚”，他不理解这些几何背后的实质，自然会觉得很难。

然而，这不该是几何该给我们留下的印象啊。我们平常接触的几何，一个点、一条线、一个正方形、一个圆，这些都是我们日常生活里一些形状的完美投射，它们非常的实在，一点都不虚。很多在代数上不好理解的东西，我们把它画到几何图形上一下子就理解了。几何原本就应该比代数更加简单直观，但是为什么到了相对论这里，大家反而觉得几何语言更加难以接受了呢？原因就是狭义相对论里使用的几何并不是我们熟知的欧式几何，而是一种全新的闵氏几何，当我们把欧式几何里的一些习惯和常识代入进来的时候，自然会引起各种水土不服。

所以，这里我们先不谈闵氏几何和欧式几何的具体区别，我们先来看看狭义相对论是怎么和闵氏几何对上眼了的。为什么狭义相对论不用欧式几何来描述，而非得使用一个我们不熟悉的闵氏几何呢？这个问题不清楚，讲再多闵氏几何的性质也是白搭。

02 两个基本假设

为什么狭义相对论要使用我们不熟悉的闵氏几何，原因当然还是得从自身来找。大家都知道狭义相对论有两条基本假设：相对性原理和光速不变。从这两个假设出发我们可以很自然的推导出狭义相对论里各种奇奇怪怪的结论，这里我们先来审查一下这两个假设。

相对性原理说物理定律在所有的惯性参考系里都是平等的，不存在一个特殊的惯性系。这一点很自然，伽利略很早就发现这点了，他意识到一个人在一个匀速移动（惯性系）的密闭船舱里根本无法区分这艘船到底是静止的还是以某个速度匀速运动。无法区分的意思就是这两个参考系（静止和匀速运动）是平等平权的，否则，你就应该有办法把它们区分开。

不同的是：伽利略只敢给力学定律打包票，他只敢说我们无法用力学实验区分两个惯性系，其他定律（比如电磁学实验）能不能区分惯性系他就不敢说了。爱因斯坦说你不敢打包票我来，我打赌所有的物理定律（力学的也好，电磁学或者其他的也好）都无法区分惯性系，你在船舱里做什么实验都也无法区分这艘船是静止的还是匀速运动的。

从这里我们可以感觉到，相对性原理好像并没有那么反常识，它只是把伽利略的那套相对性原理的适用范围给扩大了。那么，狭义相对论里那么多结论的“诡异”似乎就应该来自另外一个假设，也就是光速不变。

光速不变说真空中的光速在所有的惯性系里都是一样的。不论你在哪个惯性系（注意一定要是惯性系，非惯性系里光速就没人管它了）里测量光速，在静止的地面也好，飞速的火车飞船里测也好，测得的光速都是一个定值 c。

这就太反常识了，怎么能够在不同的参考系里测量同一个物体的速度都相同呢？比如，在一辆速度为 300km/h 的高铁上，有一个人以 5km/h 的速度朝车头走去。那么，高铁上的人会觉得他的速度是 5km/h，而地面的人会觉得他的速度是 300+5=305km/h，这两个速度肯定是不一样的。但是，如果我把这个人换成一束光，让这束光射向车头，光速不变就是说不管你是在高铁上测量，还是在地面上测量，这束光的速度都是 c。你以为在地面上测量的光速应该是 c+300km/h 么？对不起，并不是这样。

你觉得这个事诡异么？诡异！为什么会这样呢？不知道，光速不变是狭义相对论的一个基本假设，这个类似数学里的公理，我们只能假设它是对的，但是却无法证明它是对的，它的可靠性由实验保证。其实，这个事情很多人还是知道的，但是，大多数人并不知道如果我们再深挖一下光速不变原理的秘密，我们就能找到一条通向闵氏几何的隐秘通道。

03 光速不变的秘密

光速不变说你在任何惯性系中测量光速，得到的结果都是 c，我们来定量的分析一下这个原理。

假设我们在 K 系里测量一束光，假设这束光在Δt 的时间内走了Δl 的距离，那么显然就有Δl=Δt×c。如果我们把这束光在 x，y，z 三个坐标轴方向移动距离的分量记为Δx，Δy，Δz，那么根据勾股定理就有：Δl²=Δx²+Δy²+Δz²，再把这两个式子合起来就能得到：Δx²+Δy²+Δz²-（Δt×c）²=0。如果这时候我们用一个新的量Δs²表示左边的东西，那么就有Δs²=Δx²+Δy²+Δz²-（Δt×c）²=0。

好，事情发展到这里，一切都非常容易理解，上面的事情倒腾来倒腾去就是一束光在空间里走了一段距离，然后套用了小学生都知道的距离等于速度乘以时间而已。而且，大家也会发现这个事跟光速不变也没有什么关系，你就是把上面的光换成一颗子弹，把光速 c 换成子弹的速度，那么上面的一切推理都还是那样的。没错，因为光速不变说的是光速在不同的惯性系里都一样，那么我们还得再考察一个惯性系。

还是上面那束光，我们这次在另一个参考系 K’里对它进行测量。假设我们测量的结果是它在Δt’的时间内走了Δl’，我们同样对这个距离做一个分解，假设它在 x，y，z 三个坐标轴方向移动距离的分量记为Δx’，Δy’，Δz’。根据光速不变原理，光在这个参考系里的速度还是 c，那么，按照上面的逻辑，我们依然可以得到Δs’²=Δx’²+Δy’²+Δz’²-（Δt’×c）²=0。

当我们把 K 和 K’这两个参考系了的结果拿来对比的时候，光速不变原理带来的反常效应就出现了：大家有没有发现Δs 和Δs’的表达式的形式完全一致，而且值还相等（都等于 0）？

我们只是把 K 系里测量的时间和距离全都换成了 K’系里测量的时间和距离，其它的东西我们一概没动。而在牛顿力学里，Δs和Δs’的表达式形式是不一样的，因为牛顿力学里另一个惯性系的测量速度会加上两个参考系之间的相对速度。也就是说在牛顿体系里，在K’系里测量的光速应该是 c 加上两个参考系的相对速度，这样Δs’的形式就Δs跟不完全一样了，而相对论是用光速不变强制保证了它们的形式一致。

这一点大家好好想一想，它并不难理解，但是却是后面的关键。我们现在等于说是定义了一个Δs，对于光来说，这个Δs 的值在不同的参考系里是相等的，刚好都是 0。

那么，重点来了：如果我把这个Δs 从光推广到所有物体，我仍然从两个不同的惯性系 K 和 K’去测量这个物体在空间上运动的距离Δx、Δy、Δz 和时间上经过的间隔Δt，然后一样把它们组合成Δs 和Δs’。那么，这个物体的Δs 和Δs’之间有没有什么关系呢？它们是不是还跟光的Δs 和Δs’一样相等并且都等于 0 呢？

是否等于 0 很好回答，一看就知道肯定不等于 0。假设博尔特 1 秒钟跑 10 米，那么Δt=1、Δx=10，不考虑另外两个维度（Δy=Δz=0），看看Δs²的表达式：Δs²=Δx²+Δy²+Δz²-（Δt×c）²=100+0+0-（1×3×10^8）²，这显然是个非常大的负数。那么问题的关键就落在在惯性系 K 和 K’里测量的这两个值Δs 和Δs’是否相等，也就是说，如果博尔特在跑步，我们从地面和火车上测量得到的 Δs 和Δs’是否相等？

这个答案我直接告诉大家：一样！

这个证明过程其实也非常简单，这不就是同一个事件看它在不同的惯性系里是否满足某个式子么？同一个事件在不同惯性系下变换关系，在相对论里这不就是洛伦兹变换的内容么？所以，你直接用洛伦兹变换去套一下Δs 和Δs’，你很简单就能发现它们是相等的，这里我就不做具体计算了，当作课后习题。

所以，我们通过分析就得到了这样一个结论：在相对论里，不同惯性系里测量一个物体的位移、时间等信息可能不一样，但是它们组合起来的Δs²=Δx²+Δy²+Δz²-（Δt×c）²确是相等的，而这个值对光来说还刚好就是 0。

注意了，这个结论极其重要，正是它决定了为什么我们要使用闵氏几何来描述狭义相对论，甚至，从某种角度来说，它几乎包含了闵氏几何里的全部奥秘。为了让大家更好地了解这个结论背后的意义，我们先去看一看欧式几何里的类似情况。

04 欧式几何不变量

在欧式几何里也有一些量是不随坐标系的变化而变化的，比如最简单的线段的长度。

在二维的欧式几何里，我们假设在一个直角坐标系里有两点 A（x1，y1）、B（x2，y2），令Δx=x2-x1，Δy=y2-y1，那么，利用勾股定理就能非常容易的算出 AB 之间的距离Δl²=Δx²+Δy²。这时候我们如果在建一个新的直角坐标系，在这个新的坐标系里原来 A、B 两点的坐标变成了 A（x1’，y1’）、B（x2’，y2’），同样令Δx’=x2’-x1’，Δy’=y2’-y1’，AB 之间新的距离Δl’²=Δx’²+Δy’²。这时候我们可以很轻松的验证Δl=Δl’，也就是说Δx²+Δy²=Δx’²+Δy’²。

这个结论一点都不奇怪，我们都可以很直观的感觉到，为什么呢？因为欧式几何就是我们日常熟悉的空间啊，我们现在就假设有一跟 2 米长的尺子 AB，我在一个直角坐标系里计算它的长度的平方Δl²=Δx²+Δy²=2²=4，难不成我在另一个坐标系里算得它的长度的平方Δl’²=Δx’²+Δy’²还能不等于 4 么？我这把尺子的长度是一定的，如果我在不同坐标系下得到尺子的长度却不一样了，那还了得，那这几何就有问题了。

因此，在欧式几何里，Δl²=Δx²+Δy²也是一个坐标系不变量，这个值不随你取坐标系的变化而变化。很显然的，如果把欧式空间从二维推广到三维，那么这个不变量自然就可以写成Δl²=Δx²+Δy²+Δz²；推广到四维，我们用 t 表示第四个维度，那么Δl²=Δx²+Δy²+Δz²+Δt²，再往上推广几维，我就加几个分量就行了。

大家肯定注意到了：在欧式几何里，不随坐标系变化的是Δl²=Δx²+Δy²+Δz²+Δt²，而我们上面在讲狭义相对论的时候，不随惯性系变化的量Δs²=Δx²+Δy²+Δz²-（Δt×c）²。这两者非常的相似，这个光速 c 是个常数，可以不用考虑，为了方便计算我们甚至可以直接约定 c=1，这样的话Δl²和Δs²的差别就仅仅只差一个Δt 前面的负号而已。

那么，这种形式上的相似和那个负号的差别到底意味着什么呢？毕竟它们一个代表的是不随惯性系的变化而变化的量（Δs²），一个代表的是欧式几何里不随坐标系的变化而变化的量（Δl²），一个是物理量，一个是几何量，好像并没有直接的关系。但是，我们这样想想：如果我想用一种几何来描述狭义相对论里Δs²=Δx²+Δy²+Δz²-（Δt×c）²不随惯性系的变化而变化的这种性质，我们肯定就不能选欧式几何了（因为欧式几何里不随坐标系变化的量是Δl²=Δx²+Δy²+Δz²+Δt²）。所以我们需要一种新的几何，在这种新几何里，不随坐标系变换而变化的量是类似Δs²这样带有一个负号的量，这种全新的几何自然就是闵氏几何。

你这时候心里可能有点疑惑：我们真的可以只凭借不随参考系变化的量是Δs²和Δl²，就断定这是两种不同的几何么？Δs²和Δl²这些东西到底意味着什么？或者说，到底是什么决定了一种几何？

05 线元决定几何

我们从小就在学习欧式几何，我们学习直线、三角形、圆等很多几何图形，我们关心它们的各种性质，比如两点的距离、曲线的长度、两条线的夹角、一个图形的面积。但是，大家有没有想过：在欧式几何的各种各样的性质里，有没有哪个是最基本的？也就是说，我们能不能只定义这个最基本的量，其他的各种量都可以从这个量里衍生出来？这样的话，我们就只需要抓住这一个最基本量的性质，就可以抓住这种几何的性质了。

答案是：有，这个最基本的量就是弧长，准确地说是组成任意曲线、弧线的基本元段长。

要把这个说清楚，我们这里得稍微引入一丢丢微积分的思想，别慌，这个很容易理解的~在欧式几何里，我们很容易求一根线段的长度（直角坐标系里利用勾股定理就行了），但是，如果要你求一条任意曲线的长度呢？

比如上图的曲线 AB，这是随手画的很一般的一条曲线，不是什么特殊的圆弧，你要怎么求它的长度呢？数学家们是这么考虑的：我在曲线 AB 之间取一些点，比如 P1、P2、P3，然后这三个点就把这段圆弧的分成了四个部分。我们用线段把这几个点连起来，这样我们就得到了一条折线，这时候我们就用折线的长度（也就是这四条线段的和 AP1+P1P2+P2P3+P3B）来近似代替曲线 AB 的长度。当然，你肯定会说，曲线的长度明显比这四条线段加起来更长啊，你怎么能用折线的长度来代替曲线呢？

是的，如果你只在 AB 之间取三个点，那么曲线 AB 的长度肯定要比折线的长度多很多，这样近似的误差很大。但是，如果我再多取一些点呢？我在 AB 之间取十个、一百个甚至一千一万个点，那么，这成千上万条线段组成的折线的总长度跟曲线 AB 比呢？当然，还是会短一些，但是，你可以想象，这时候这些折线已经跟曲线 AB 非常接近了。如果一根 1 米长的曲线被你分成了 1 万条线段，这时候你用肉眼根本分辨不出来这是原来的曲线还是折线。但是你内心还是知道折线要短一些，那么接下来就是重点了：如果我在曲线 AB 之间放无穷多个点呢？

无穷是一个很迷人，同时也很迷惑人的词汇。从上面的分析我们知道：当我们在曲线 AB 里放越多的点，这些小线段连起来的折线就越接近曲线 AB 本身。那么，当我们放了无穷多个点的时候，这无穷多个线段组成的折线是不是就应该等于曲线 AB 的长度了？答案是肯定的，而这，就是微积分最朴素也是最核心的思想。

在这种思想的指导下，我们要求任意曲线的距离，最终还是要求小线段的距离，因为无穷多个小线段累加起来的长度就是曲线的长度。因此，我们只要知道如何求无穷小的线段的长度，我们就能用微积分的思想求出任意曲线的长度，我们把这个最基本小线段称为曲线的一个元段长，记做dl。

在欧式几何里，我们把基本元段 dl 在坐标系里分解一下，用 dx 和 dy 表示 dl 在 x 轴和 y 轴上的分量，那么根据勾股定理就有dl²=dx²+dy²，我们就把dl²称之为线元。

提炼出了线元这个概念以后，我们就可以开始反推了。在任何一种几何里，如果我们确定了线元，就等于知道了元段dl的长度，然后就可以利用上面微积分的思想求任意一段曲线的长度。那么，接下来，我们会发现几何里的其他性质都可以按照这些定义。比如，我们就可以把两点之间的距离定义为这两点之间所有可能的曲线里最短的一条，把两条直线的夹角定义为弧长和半径的比值（想象在一个圆里，半径固定，弧长越大角度越大），其他什么面积、体积之类的几何性质就都可以根据这些基本性质来定义。

最后，你会发现只要给定了一个线元，我们就能把它所有的几何性质都确定下来，也就是说：线元决定几何。

那么，什么是欧式几何呢？欧式几何就是由欧式线元（dl²=dx²+dy²）决定的几何。非欧几何呢？只要你的线元不是欧式线元，那么这个线元决定的几何就是非欧几何。用这种新线元，我们一样可以定义出在这种新几何里的曲线长度、两点的距离、线的夹角等等几何性质。

那么，闵氏几何是什么？闵氏几何的线元又是什么呢？

答：很显然，闵氏几何就是由闵氏线元决定的几何。闵氏线元是这样的ds²=-dt²+dx²+dy²+dz²，如果只考虑二维闵氏几何的话，那么ds²=-dt²+dx²。

闵氏线元（ds²=-dt²+dx²）跟欧式线元（dl²=dx²+dy²）十分相像，它们之间唯一的差别就在于闵氏线元的第一个分量 dt²的前面是负号，而欧式线元全部都是正号。也因为如此，闵氏几何跟欧式几何也非常像，所以闵氏几何还有一个称呼，叫伪欧几何。但是，我们也要特别注意这个负号，正是这个负号，决定了闵氏几何和我们熟悉的欧式几何里所有不一样的地方，而这些不一样，恰恰是我们通过闵氏几何来理解狭义相对论的关键。

06 闵氏几何与狭义相对论

我们现在知道了，所谓的闵氏几何，不过是由闵氏线元ds²=-dt²+dx²+dy²+dz²决定的几何。在这种几何里面，曲线的长度、两点的距离、线的夹角等一切性质都有这个第一项带了一个负号的闵氏线元决定。

看看这个闵氏线元ds²=-dt²+dx²+dy²+dz²，再看看我们最开始提到的那个在狭义相对论里不随惯性系的变化而变化的量Δs²=Δx²+Δy²+Δz²-（Δt×c）²，是不是非常像？在相对论里有两种单位制：国际单位制和几何单位制。国际单位制就是我们平常熟悉的那一套单位制，几何单位制就是选择光速 c=1，这样可以大大简化在用几何处理相对论问题的难度。采用几何单位制的话，不随惯性系变化的Δs²=Δx²+Δy²+Δz²-Δt²，这就真的跟闵氏线元ds²=-dt²+dx²+dy²+dz²一模一样了。

这就是为什么我们要用闵氏几何，而不是欧式几何来描述狭义相对论的根本原因。

在牛顿的世界里，时间是绝对的，三维的空间也是绝对的，一根木棒在三维空间里随便怎么变换，随便怎么变换参考系，它在三维空间里的长度是一定的，这个是跟三维的欧式线元对应的（因为三维的欧式线元 dt²+dx²+dy²也不随坐标系的变化而变化）。

但是，在狭义相对论里，空间不再是绝对的，不再是一成不变的，我们熟悉的尺缩效应不就是说从不同的惯性系里观测同一把尺子，这个尺子的长度是不一样的么？这就是说空间上的“长度”在狭义相对论的不同惯性系里不再是不变量。但是，我们发现如果把时间也考虑进来，把三维空间和一维时间一起组合成四维时空，那么这个四维时空里的间隔Δs²=Δx²+Δy²+Δz²-Δt²就是不随惯性系的变化而变化的量（这个在前面说过，用洛伦兹变换可以非常方便的证明）。

所以，在牛顿的世界里，三维空间是绝对的，他必须保证同一把尺子在不同的三维空间的坐标系里长度是一样的，也就是说在度量三维空间里长度的方式（这个有个更专业的概念叫度规，这里我们知道就行）必须跟坐标系无关，而欧式几何正好有这样的特性，所以牛顿力学的背景是欧式几何。

而在狭义相对论里，三维空间并不是绝对的，三维空间里一把尺子的长度在不同惯性系里是不一样的。但是，三维空间和一维时间组成的四维时空是绝对的。四维时空里如果也有这样一把“尺子”，那么这把“尺子”无论从哪个惯性系来看，它的四维“长度”都是一样的。而狭义相对论的这种四维“长度”，或者说我们在四维时空里度量长度的方式，它跟闵氏线元表达式的形式是一样的。也就是说只有在闵氏几何里，狭义相对论的时空间隔才对应于他们几何里的“长度”的概念，所以我们要使用闵氏几何来描述狭义相对论。

理解这一段非常的重要，因为只有理解了这个，你才能从根本上把闵氏几何和狭义相对论对应起来。有很多闵氏几何的科普文章里上来就是直接给你画时空图，然后告诉你闵氏几何里的这种图形这个几何性质对应着狭义相对论里的这种概念，这样很多人就感觉难以接受，然后对几何语言产生抵触的心理。

好，既然我们打算用闵氏几何来描述狭义相对论，那么肯定就要把狭义相对论里的物理语言翻译成闵氏几何里的几何语言。几何肯定是离不开画图的，在欧式几何里我们经常会画出一个几何图形在空间上的样子，这是空间图。而狭义相对论把时间和空间看作一个整体， 它要求我们以同等的地位来看待时间和空间，所以我们需要画出一个事件同时在时间和空间里的样子，这种图就叫时空图。

07 时空图

在时空图里，你能非常自然地感觉到时间和空间被统一起来了，因为时空图里的时间轴和空间轴有着完全的平等的地位。

在时空图里，一个粒子现在在哪，你找到它的空间坐标（x，y，z），记下现在的时间 t，那么你就得到了它的时空信息（x，y，z，t），那这个时空信息就对应时空图里的一个点，这就叫时空点。

同样的，你再记下它下一个时刻 t1 的位置（x1，y1，z1），那么它又对应了坐标系的另一个点（x1，y1，z1，t1）。所以，一个粒子在任一时刻的时间、空间信息就都对应了时空图里的一个点。那么，如果考察这个粒子的全部历史，你就可以得到一系列的这种时空点，这些点在时空图里就会形成一条线，这条能代表粒子全部历史的线就叫粒子的世界线。

现实生活里一个粒子有四个维度（三维空间 + 一维时间），那么对应的坐标轴应该也是四维的，但是我们在二维平面里勉强可以画出三维图形，对四维图形实在无能为力。为了方便起见，我们假设粒子只沿 x 轴方向运动，这样我们就可以不考虑 y 轴和 z 轴的情况，从而把四维的问题简化为二维，然后我们就可以很愉快的在一张二维的纸上画这二维时空图了。

我们先建立一个坐标系，横轴 x 代表粒子的空间信息，纵轴 t 代表粒子的时间信息。为了再次简化问题，我们采用几何单位制，也就是取光速c=1，然后我们再来看一些具体问题。

问题 1：一个静止不动的粒子在时空图里是什么样的？或者说它的世界线是什么样的？

这个答案很容易想到，一个粒子静止不动，就是在空间上没动，那么它的 x 坐标一直为零，但是时间依然在流逝，也就是粒子的时间坐标在一直变大。所以，静止不动的粒子是世界线是一条跟 t 轴重合，垂直于 x 轴的直线。

问题 2：一个匀速向右运动的粒子的世界线是什么样的？

这个也不难想象，一个匀速向右运动的粒子，它在时间轴不停往上走的同时，空间轴上也在不停地往右走，那么这个粒子的世界线应该是一条斜直线。问题是，斜多少？是所有的坐标空间它都可以斜，还是有什么限制？这个问题我们先放着，先看看第三个问题。

问题 3：一条朝右上方 45°的斜直线（如下图的 L1）代表了什么粒子的世界线？

我们先来算一算这个粒子的速度：我们在粒子的世界线 L1 上取两个点，也就是假设粒子在 t1 时刻在位置 x1，在 t2 时刻在位置 x2。因为这条直线是 45°的，所以很显然 x2-x1=t2-t1，.那么粒子的速度v=(x2-x1)/(t2-t1)=1。

速度等于 1 是什么意思？我们在画图的时候采用的是几何单位制，也就是取光速 c=1(如果我们不采用几何单位制，那么竖轴的单位就不是 t，而是 ct，本质并没有什么不同)。现在这个粒子的速度等于 1，其实就是代表这个粒子的速度是光速，速度是光速那自然就是光子了，那么这条 45°斜直线就代表了光子的世界线。

从这里我们可以看到，在时空图里，光子的世界线是 45°的斜直线。我们也知道在相对论里任何有质量粒子的速度都是小于光速的，那么一个有质量的粒子做匀速直线运动的世界线该是一条什么样的斜直线呢？是在区域 1还是区域 2？

我们可以这样想一下：如果粒子的速度比光速小，那么假设粒子在 t1 时刻在 x1 处，那么到了 t2 时刻它肯定到不了 x2 地方，那么这两点的连线肯定就在 L1 的上方，也就是区域 1。其实我们也可以想一个极端的粒子，假设这个粒子在原点不动，那么粒子的世界线就是跟 t 轴重合，粒子速度到达光速就是 45°的那条直线，那么速度在静止和光速之间的粒子世界线自然就是在区域 1 的斜直线了。

现在我们知道了这样一个结论：在时空图里，45°的斜直线代表了光子的世界线（如 L1），比光子世界线更陡，更加靠近 t 轴的斜直线（如 L2）是有质量粒子匀速直线运动，或者说惯性运动（速度小于光速）的世界线。

有了这样的基本认识，我们来用几何语言分析一下狭义相对论里入门教材里必定会碰到的问题：火车闪光问题。这个问题之所以重要，是因为它揭示了同时的相对性，也就是说在一个惯性系看来是同时发生的事件，在另一个参考系里不一定是同时发生的。爱因斯坦敏锐地发现了这点，然后借此从看似牢不可破的牛顿力学里撕开了一道口子。

08 同时的相对性

在牛顿力学里，时间是绝对的，所以同时必然也是一个绝对的词汇。在一个参考系看来是同时发生的事件，不管谁来看都绝对是同时发生的，这也是一个非常符合常识的论述。

但是，爱因斯坦用一个简单的火车实验就让人们的这个信念坍塌了，这个实验是这样的：假设地面上有一辆匀速运动的火车，在某一个时刻，地面上的观察者发现这个火车的车头和车尾同时被闪电击中。也就是说，对于地面参考系而言，闪电击中车头和车尾这两个事件是同时发生的。但是，爱因斯坦认为在火车参考系里，这两个事件就不是同时发生的。

原因也很简单，我们假设在闪电击中火车头尾的时候，在地面这两点的中点有一个观察者。因为两个事件在地面系看起来是同时发生的，所以，站在地面中间的那个观察者肯定会同时看到车头和车尾发过来的闪光，所以这两个事件是同时的。

但是，站在火车中间的观察者就不是这样了，因为车头车尾的闪光在向中间传播的时候，火车本身也在前进，所以火车中间的人就会先看到车头发过来的闪光，后看到车尾发过来的闪光。所以，火车上的观察者就会觉得这闪电击中车头和车尾这两个事件不是同时发生的，而是击中车头的先，击中车尾的后。

爱因斯坦从这个火车闪光实验出发，发现了同时的相对性，进而打开了狭义相对论的大门。这个实验比较简单，整个逻辑过程也不复杂，但是这样讲不够直观，不够具有普遍性。因为很多人会把这个实验当做一个特例来处理，也就是只有当他们意识到要讲同时的相对性的时候才会想起这个实验，平常就会把这个实验带来的同时的相对性给忘了，然后带来一系列的“相对论诡异疑难”。下面我们从几何语言来看看这个问题，看看如何让这个重要问题更直观，更具有普遍性。

我们假设闪电同时击中车头车尾（从地面系观测）的时候，火车的车尾 M’、车头 N’刚好经过地面的 M 和 N 点，P 点为地面 MN 的中点，P’为火车上的中点，我们来看看怎么在时空图上描述这个闪电击中火车的问题。

我们先来看看地面上 M 和 N 点的世界线，因为 M、N 在地面上没有动，所以 M 和 N 点的世界线都是一条沿着时间轴 t 竖直向上的直线（空间位置没动，只有时间 t 在动）。同样的，在 MN 中间的 P 点也没动，它的世界线也是一条竖直向上的直线。这三条线好画，那么在火车上的 M’、N’和 P’，它们都在做匀速直线运动，那它们的世界线是什么样的呢？这个我们上一节刚好说了，做匀速运动的粒子的世界线是一条比 45°线更陡的斜直线。那我们把这六个点的世界线都画出来，不难理解应该就是下面这样（横轴为空间 x，纵轴为时间 t，这里省略了）。

下面是关键的了，怎么画车头、车尾的闪光向中点传播的过程？我们知道，闪电击中车头车尾之后，这个事件就会向四面八方发射光信号（所以四面八方的人都能看到火车被闪电击中了），但是，其他的信号我们都不关心，我们只关心被地面中点 P 和火车中点 P’所接收到的那一束光信号。那么，这个光信号要怎么画呢？它们的出发点肯定在 m 和 n，那接下来呢？这次我们再次想起了上一节中提到的：光子的世界线是 45°的斜直线。那么我们就加上这两条 45°的世界线，最后的图就是下面这样的。

这两根世界线跟两个中点 P、P’的世界线产生了三个交点 A、B、C，这是三个很有意思的点，我们来分析一下它们的物理含义。

首先是 A 点，A 点是闪光世界线跟地面中点 P 点的世界线交点，它们相交了是什么意思？纵轴代表时间，横轴代表空间，相交了就代表这两个粒子此时时间和空间信息都一样，都一样那就是相遇了啊，具体到我们这个问题就是闪光传播到了地面上的中点。因为地面没有动，M 和 N 点到 P 点的距离又是一样的，那么车头车尾的闪光肯定同时到达地面中点，所以它们都相交于 A 点是正确的。

再来看 B 点和 C 点。B 点是车尾的闪光的世界线和火车里面的中点 P’世界线的交点，那B 点代表的意思自然就是火车中间的观察者观察到车尾的闪光这个事件。同理，C 点是车头闪光世界线跟 P’世界线的交点，那C 点就是火车中间的观察者观察到车头闪光的这个事件。这样看就非常明显了，纵坐标是时间轴，那么 B 事件明显就是在 C 事件之后发生的啊。

这正是同时的相对性的表现：对于地面系，它们都交于 A 点，所以是同时的；对于火车系，它们分别交于 B 点 C 点，所以是不同时的，这在时空图里极为直观。

这里有一个事要强调一下：我们在这个火车闪光问题里虽然涉及到了地面系和火车系，但是我们是一直在地面系来分析问题的。我们画的时空图，不管是地面上的点还是火车上的点，我们都是在地面系画，因为毕竟一张图只有一个坐标系嘛。那么，我们能不能在一张图里同时把地面系和火车系两个惯性系都画上呢？

答案当然是可以的。

09 两个坐标系

我们来具体看看这个问题：假设我们现在已经画了一个地面系的直角坐标系 x-t，那么我们要如何把火车系的坐标系 x’-t’画出来？

第一次遇到这个问题的同学可能有点懵，不着急我们一步步来，我们先看看火车系的纵轴 t’要怎么画。要画火车系的纵轴，我们先想想一个坐标系的纵轴的是什么意思？我们知道如果我们让一个点的横坐标为零，那么这个点的轨迹就是跟纵轴重合的。还记得我们上面说的静止粒子的世界线么？静止粒子的空间坐标 x 为 0，所以它的世界线就是垂直于 x 轴，与 t 轴重合的一条直线。那么，火车系的 t’轴自然也是在火车系里静止在原点处粒子的世界线。

这一点很重要，大家好好理解一下，也就是说我们只要把火车系处于原点处粒子的世界线画出来，我们就能得到火车系的 t’轴。那么，一个在火车系静止的点，在地面系看来它是在做匀速直线运动，而匀速直线运动的点的世界线，我们上面也说了，就是一条比 45°更陡的斜直线。所以，火车系的 t’轴就是这样一条更陡的斜直线，如下图所示：

火车系的 t’轴画好了，那火车系的 x’轴呢？大家可以看到我在图上用虚线画了一根与 t’垂直的轴，并且特意标明了“错误的 x’轴”。为什么要这样标呢？因为这是相对论初学者极容易犯的错误。我们已经习惯了欧式几何，欧式几何里直角坐标系都是相互垂直的，所以到了这里很多人看到我们已经画出了 t’轴，就立马条件反射地画一根和 t’轴垂直的当做 x’轴，但是这是错误的，为什么呢？

这里我们第一次感受到了闵氏几何的异样。我在最开始花了那么大的篇幅告诉大家为什么狭义相对论要使用闵氏几何，我们也知道了闵氏几何的线元跟欧式几何不一样（时间项前面多了一个负号），所以，我们在画时空图处理狭义相对论问题的时候，一定要意识到自己虽然是在欧式平面里画图，但是我们画的是闵氏几何里的图形。

有人可能会有点疑问，我们前面不是已经用时空图解决了同时的相对性问题么？我们不是已经把爱因斯坦火车闪光问题用时空图画出来了么，我没感觉啥异样啊？那只是因为那个问题比较简单：它只有一个坐标系，而且也不涉及到线长相关的问题，所以我即便在一个欧式直角坐标系里把它画出来了，它也暂时没什么冲突。如果我们生活在一个闵氏空间里，那么我们画出的闵氏直角坐标系肯定都是相互垂直的，但是我们生活在欧式空间里，我已经用一个欧式空间里的直角坐标系画了一个闵氏坐标系，那么另一个就肯定不可能再是垂直的了。

这里的逻辑有点绕，大家可以细细品味，搞得不是很懂也不要紧，我接下来会把另一个坐标系画出来，大家能看懂再回去看上面的一段话就明白了。

好，回到正题，我们再来看看火车系正确的 x’轴该怎么画。我们再来整体回顾一下这个事情：我们现在是已经画好了地面系 x-t，要画火车系 x’-t’，火车系和地面系它有没有什么关系呢？有啊，洛伦兹变换说的不就是地面系和火车系的关系么？什么是洛伦兹变换？比如我在地面系观测到了一个粒子的位置和速度，现在我想知道它在火车系里是什么情况，我并不需要重新再到火车系里测量一遍这个粒子的位置和速度，我只需要根据洛伦兹变换就可以直接得到火车系里那个粒子的运动情况。所以，洛伦兹变换就是两个惯性系之间的联系，我只要知道了一个惯性系里粒子的运动情况，立马我就可以知道其他惯性系里粒子运动的情况。

所以，我们可以根据洛伦兹变换来找到两个惯性系之间的联系。我现在不是根据地面系的坐标轴来找火车系的坐标轴么？我们对着洛伦兹变换改就是了。洛伦兹变换是下面这样的：

其中，x，y，z，t 代表地面系里观测到的，x’，y’，z’，t’是火车系里观测到的。v 是火车系相对地面系的速度，火车的速度一旦给定了，这个 v 就是一个定值，c 是光速，所以右边的γ都是一个常数。如果我们再根据几何单位制来，取c=1，那么洛伦兹变换就可以简化成下面的样子：

因为我们只考虑火车系相对地面系在 x 轴方向上的运动，所以在 y 和 z 方向上还跟原来一样，我们可以不考虑。我们现在画图也是来画 x-t 图，所以我们重点关注这两个式子：

这是什么呢？这不就是火车系了的 x’和 t’么？我现在要画的就是 x’的坐标轴，也就是火车系的空间坐标轴，那怎么找到这个坐标轴呢？这个我们前面也提过：纵坐标的那条线就是横坐标为 0 的所有点的集合，反过来也是，横坐标就是纵坐标为 0 的点的集合。所以，我们令火车系的时间等于 0，也就是纵坐标 t’=0 就能找到横坐标 x’轴了。

那我们令t’=γ（t-vx）=0，因为γ是一个不为零的常数，所以就只有 t-vx=0 了，也就是t=vx。

这在 x-t 坐标系里就是一条过原点的直线，斜率为火车的速度 v（斜率就是这条直线的倾斜程度，你可以理解为一个坡越陡斜率越大。当直线与横轴重合的时候，斜率为 0；当直线跟横轴成 45°的时候，斜率为 1；当直线跟纵轴重合的时候，斜率为无穷大）。因为我们这里是几何单位制，光速为 1，在狭义相对论里任何有质量的物体它的运动速度都是小于光速的，所以火车的速度 v 肯定是小于 1 的，也就是说这条直线的斜率比 45°的直线（刚好是光的世界线）小。

再者，我们可以用同样的方法令x’=γ(x-vt)=0，就能得到火车系的纵轴是这样一条直线：t=x/v。它的斜率是 1/v，因为 v 小于 1，所以 1/v 是个大于 1 的数，所以这条斜直线的斜率比 45°要大（我们前面画的也正是这样）。这里我给一个初中数学的结论：斜率互为倒数（比如 v 和 1/v）的两条直线它们是关于 y=x，也就是 45°的直线对称的。所以，我们的 x’轴是跟 t’轴关于 45°的直线对称的。这样我们就能精确地把它画出来了，如下图：

第一次看到这样一个坐标系的同学可能会感觉非常别扭，为什么火车系 x’-t’的坐标系不是正交的，不是一个直角呢？我们得这样看：它们是正交的，只不过它们是在闵氏几何里正交，我们现在强行把它画在欧式几何里，那么肯定就看起来不正交了。

还有同学也会有疑惑，你不是说狭义相对论里惯性系都是平权的么？那么为什么这里把地面系画成直角的，而把火车系画成了一个小于直角的坐标系？我要是人就在火车里，我非要把火车系画成直角的，不行么？行，当然行。你可以按照上面的思路把火车系画成直角的基准系，再反推过去画地面系，最终的两个图虽然形状不一样，但是实质上还是等价的。

理解这个双坐标系非常关键，它第一次向我们展示了闵氏几何不一样的地方。有了它，我们就可以很方便的处理不同惯性系里的一些事情，比如，我们喜闻乐见的尺缩效应。

10 尺缩效应

尺缩效应是狭义相对论里比较有趣的一个效应，它简单说来就是一句话：运动的物体长度会收缩，也就是动尺收缩。但是这样描述会让许多初学者心生疑惑，你动尺收缩是真的收缩了还是只是看起来收缩了？这是一种观测效应还是一种由于光速有限造成的传播误差？你相对尺子没动，觉得尺子没缩，我觉得缩了，那么它到底缩了没有（这是个很常见的错误的问题）？

其实，用非几何语言初学相对论的人不可避免地会遇到很多类似这样的问题。因为大家在牛顿的那一套环境里浸润久了，想一下子把思维切换过来很麻烦。而且学相对论的人最容易载到“相对”两个字里来，该相对的东西不相对，不该相对的东西又跑去相对，最后把自己绕进去了。但是用几何语言却没有这样的烦恼，因为有很多物理量在 3 维的时候是相对的，在 4 维里就都是绝对的了。而且，几何图形清晰直白，会大大降低这类问题的难度和迷惑性。

好，现在我们来看看怎么用几何语言处理尺缩效应。

一个粒子的世界线是一条线，而一把尺子是由许多粒子组成的，所以一把尺子在时空图里留下的轨迹就应该是一个面，我们称之为尺子的世界面。我们还是以地面系为基准系，假设尺子相对地面系静止，那么尺子每个粒子的世界线都是一条平行于 t 轴的线，合起来它的世界面应该是一个有一定宽度的面。上一节我们已经学会了如何把运动的惯性系也画出来，我们再把相对尺子运动的参考系 x’-t’（假设为火车系）画出来，总的时空图就是这样：

如上图所示，阴影部分就是在地面系静止的尺子的世界面，它跟 x 轴的交点为 a，跟 x’轴的交点为 b。那么我们很容易就能知道oa 就是尺子在静止地面系的长度，ob 就是尺子在运动的火车系 x’-t’的长度。

为什么呢？你想想 oa 代表什么意思？oa 就是当地面系的时间为零的时候尺子在空间 x 轴的投影，那这显然就是尺子的长度了。那么，同样的道理，因为运动的火车系的坐标是 x’-t’，ob 也是当 t’都为 0 的时候尺子在 x’轴的投影，所以 ob 就是运动的火车系测得的尺子长度。

所以，尺缩效应就变成了比较 oa 和 ob 的长度。很显然，oa 和 ob 的长度肯定不一样，那么到底是 oa 长还是 ob 长呢？

没错，你的眼睛没有看错，我就是在问到底是 oa 长还是 ob 长？可能这个时候你的脑袋是懵的，明明 oab 组成了一个直角三角形，ob 是斜边，斜边肯定比直角边更长啊，这是初中生都知道的，ob 比 oa 长难道还有什么疑问么？

没错，搁在欧式几何里，斜边大于直角边这绝对毫无疑问。但是，我们始终要记住我们处理狭义相对论问题用的是闵氏几何（否则也不会出现 x’-t’这样看起来不正交的坐标系），那闵氏几何里要怎么样比较两条线段的长短呢？

这个时候你可能意识到了：我们在闵氏几何里连怎么定义线段的长度都不知道，更别提比较两条线段的长短了。那么，闵氏几何里一条线段的长度是怎么定义，怎么计算的呢？

11 闵氏几何的线长

在讨论怎么定义，计算闵氏几何一条线段的线长之前，许多人可能对为什么这个问题会是一个问题都心存疑惑：线段的长度不就是用尺子去量一下线段么，为什么还需要什么定义？即便我不用尺子去量，一条线段我在直角坐标系里把它投影到 x 和 y 轴，假设它在 x 轴和 y 轴的投影长度分别是Δx 和Δy，那么我就可以利用勾股定理很简单的算出这条线段的长度 L²=Δx²+Δy²。

但是，我还是得再强调一次：你能这样做，是因为你已经假设了你是在欧式几何里。只有在欧式几何里，一条线段的长度才可以这样用勾股定理去计算，但是狭义相对论的几何背景是闵氏几何。为了让大家能更直观的了解，我们先不谈闵氏几何，我们就来看看球面几何。

球面几何顾名思义就是在在一个球面上的几何。你可以想象在一个篮球的表面，或者地球的表面上有两个点，那么，这两个点之间的距离应该是一段圆弧长，而不再是欧式几何里的直线。你想想，在这种情况下，你还能用勾股定理去计算这两点之间的距离么？你要硬用勾股定理去计算，那么算出来的是这两点之间的直线距离，并非在球面上的圆弧长，这显然是不对的。就好比你在地球表面计算北京到深圳的距离，你用勾股定理算出来的距离是在北京地底下打一个直线隧道通到深圳的距离，这显然不是你在地球表面从北京直线开车去深圳的距离。

从这里我们能直观地感觉到：在不同的几何里，长度的计算方式是不一样，每一种几何都有自己度量长度的规则（这就是度规），一旦这种规则确定了，这种几何也就确定了。其实，这一点我在「线元决定几何」这一节里已经说得非常明确了，不光是线长，所有的几何性质都是由线元决定的，不同的几何拥有不同的线元，自然就拥有不同的计算线长的方式。

二维欧式几何的线元是dl²=dx²+dy²，二维闵氏几何的线元是 ds²=-dt²+dx²。二维欧式几何里线段长度的计算公式是这样的：

那么，二维闵氏几何里线段长度的计算公式自然就是这样的：

因为闵氏几何的线元的时间项前面有个负号，所以，为了避免根号里面的值出现负数从而让式子无意义，我们套了一个绝对值（它保证所有值都是非负的，比如 -5 的绝对值为 5，记做|-5|=5）的符号。

也就是说，我们在闵氏几何里是根据这个式子来计算一条线段的长度的，Δt 和Δx 分别代表这条线在 t 轴和 x 轴的投影。这个式子跟欧式几何的距离计算公式很类似，唯一的不同还是时间项前面的那个负号。也正因为这个负号，闵氏几何里的线长问题才会变得更我们平常想的不一样。为了让大家熟悉一下这种新的线长计算方式，我先来举个简单的例子。

问题 4：大家还记得光子的世界线是一条 45°的斜直线把，我们现在随便在光子的世界线里取 A、B 两点，那么线段 OA、OB 的长度分别是多少呢？如下图所示：

我们先来看看 OA 的长度，因为这条直线是 45°，所以 A 点在 x 轴和 t 轴上投影得到的距离就是一样长的，也就是Δt 和Δx 的大小是一样的。但是，闵氏几何里线段长度的计算公式是它们两个相减再开根号，现在这两个值是相等的，那么相减的结果不就是 0 了么？再开根号结果自然还是 0。

也就是说，OA 在闵氏几何里的长度为 0。

你没有看错，它的长度就是 0。OA 你看着有这么长的一段，但是它在闵氏几何里的长度却是 0，这就是那个负号带来的效果。同样的，你可以接着去算 OB 的长度，或者直接算 AB 的长度，你会发现它的长度一样全部都是 0。

所以，我们有这样的结论：光子的世界线长度恒为 0。这很反直觉吧？我们再来看个例子。

问题 5：还是上面的图，我过 B 点做一条垂直于 t 轴的线，然后随便在 BC 之间取一条点 D。那么 OC 就是静止不动的粒子的世界线，OD 就是一条匀速直线运动的粒子的世界线，OB 是光子的世界线，那么它们三个的长短怎么比呢？

乍一看，好像的OB>OD>OC。但是我们刚刚算过了光子世界线 OB 的长度为 0；OC 是静止不动的粒子的世界线，那么它在空间上的位移Δx 就为 0，那么 OC 的长度就是粒子在时间轴里走的长度；OD 在时间轴上的投影跟 OC 一样，但是它的Δx 不等于 0，那么它们相减（-Δt²+Δx²）之后的数值肯定就变小了，那么 OD 是小于 OC 的。于是，我们得到的结论确实跟之前的感觉截然相反的，三者的长度是OC>OD>OB=0。

所以，当我们在说时空图了某一条曲线的长度的时候，我们都要意识到我们是用闵氏几何那把尺子（时间项前面有负号）来度量曲线的长度，这跟我们平常生活里感受的（欧式几何度量长度）是不一样的。一开始大家会觉得这种方式非常不习惯，但是一旦习惯了就会觉得这个非常自然。

好了，这里我们介绍了闵氏几何里线长的定义和计算方法，理论上我们就可以计算任意一条线段的长度了，也能比较两条线谁长谁短了。我们上一节不就是最后把尺缩效应归结比较两条线段 oa 和 ob 的线长么？那现在可以直接比了啊。

我们看到 ob 在 x 轴的投影跟 oa 是一样长的，但是 oa 在 t 轴的投影为 0，ob 在 t 轴的投影却大于零。但是，根据闵氏几何的线长公式，线长是这个线段在时间轴 t 和空间轴 x 投影长度平方相减再开根号。既然两条线段 oa 和 ob 在空间轴 x 上的投影都一样，那么在时间轴 t 上投影长度越大的，相减之后得到的值就越小，那么最后的线长就越小。

所以，我们能直接就这样感觉到，在闵氏几何下，ob 是比 oa 更短的。而ob 代表的是运动参考系下尺子的长度，oa 是静止参考系下尺子的长度，既然 ob 比 oa 更短，那么就是说在运动参考系里尺子的长度更短，这就是我们常说的尺缩效应。

这里我们是直接用线长的计算公式算出 oa 和 ob 的长度然后再来做比较，虽然算出来了，但是可能不是很直观。在许多教材和文章里都会提到另外一种看起来更直观的比较方式，那就是使用校准曲线，很多人也经常看到这个但是不是很明白，我这里就一起再讲一下。

12 校准曲线

校准曲线其实是回答了这样一个问题：闵氏几何里，到原点距离相等的点组成的轨迹是什么？

老规矩，我们先看看欧式几何的情况。在欧式几何里，到原点距离相等（比如说都等于 2）的点组成的轨迹是什么呢？这个我们都知道，这就是一个圆，到定点的距离等于定长的点的集合就是圆，这个点就是圆心，这个定长就是半径。

在欧式几何里，如果一个点（x，y）到原点的距离为 2，那么，根据勾股定理我们就可以很容易写出下面的关系：x²+y²=4。而学过一点解析几何的人就都知道，这就是圆的坐标方程。

那么，再回到闵氏几何，在闵氏几何里到原点的距离为 2 的点组成的轨迹是什么呢？其实也简单，我们不是已经有闵氏几何的距离公式了么？代入进去就行了，因为是求到原点的距离，所以Δx 和Δt 就分别是点的坐标 x 和 t，如下图：

我们把两边平方展开就得到了：

大家对比一下，这个x²-t²=4跟我们在欧式几何里圆的方程只有一个符号的差别（因为坐标轴不同，作为纵轴 t 和 y 是完全等价的）。这个式子，学过高中数学的同学一眼就能看出来这是一条双曲线，没学过或者忘了的可以自己去找一些具体的点描上去（自己找一些 x 的值，然后去算 t 的值，最后把（x，t）组成的点画到坐标系上去，看看轨迹是什么）。我这里用GeoGebra（这是一个免费的在线数学绘图工具，你输入函数或者方程，它就会自动把对应的图像画出来，有兴趣大家自己也可以去画一画）给大家画了一个图，大家可以看看，双曲线大致就是这么一个形状：

我们先甭管双曲线在欧式几何里的各种几何意义，我们是怎么得到这个图的？我们是在闵氏几何里找距离原点距离相等（这里等于 2）的点的集合，也就是说，你别看这个曲线是弯弯曲曲的，但是在闵氏几何里，这个曲线里所有的点到原点的距离都是相等的，都等于 2。

因为这种曲线上所有点到原点的距离都相等（闵氏几何下），所以我们就可以用这种曲线当作一个标准来校准，这就是把它叫校准曲线的原因。还是那个尺缩效应的图，这次我们用校准曲线来看一下。

大家看到，我加了一条过 a 点的校准曲线，我们假设它跟 x’轴交于 c 点。这样就非常清楚了，什么是校准曲线？校准曲线就是闵氏几何里到原点的距离都相等的点，因为 a 和 c 都在曲线上，所以，在闵氏几何里 oa 和 oc 的长度是相等的，也就是oa=oc。而 b、c 两点都在 x’轴上，很显然的ob<oc，合起来就是ob<oc=oa，那我们就很自然地得到了 ob 的长度比 oa 更短的结论。

而 oa 就是在静止的地面系观测得尺子的长度，ob 是在相对尺子运动的火车系上观测到尺子的长度。我们得到的结论是 ob<oa，这不就是说在运动的参考系里观测到的尺子的长度更短么？完美符合尺缩效应的结论。

在狭义相对论里经常跟尺缩效应一起出现的还有一个钟慢效应，它说相对钟运动的参考系观测钟会觉得它走地更慢一些，也就是动钟变慢（这个不同于广义相对论里引力钟慢效应说的引力越大，时间越慢）。但是钟慢效应和尺缩效应在时空图的处理上是类似的，所以我这里就不说了，大家可以自己去画一下，想知道答案的可以参考梁灿彬老师《从零学相对论》的 4.2 节（没有资料的可以回复“梁灿彬”或“梁老师”，获取《从零学相对论》+《微分几何入门与广义相对论》以及梁老师配套的的教学视频）。

接下来，我们来看一个狭义相对论里让无数新人头痛不已，也让无数科普者无比心烦的一个问题。这个问题用几何语言处理极为简单，但是读者不认，他们不太了解闵氏几何，更无法理解几何图形里代表的物理实质，你凭什么用这个这个就代表了那个那个？但是，这个问题如果用传统的代数语言讲就极为复杂，而且逻辑非常绕，一不小心就在各种相对里面把自己都绕进去了，分析它简直是对智商极大的挑战。没错，这就是大名鼎鼎的“双生子佯谬”问题。

13 双生子佯谬

双生子佯谬的描述倒是非常简单：假设地球上有一对双胞胎，有一天哥哥驾着宇宙飞船去太空里里飞了一大圈再返回地球。那么按照狭义相对论，我们就会发现哥哥再次回到地球的时候他会比弟弟更年轻。比如说，哥哥从地球出发的时候，这对双胞胎都是 20 岁，现在哥哥在太空飞了一圈再回来之后，有可能弟弟已经 30 岁了，哥哥才 25 岁。当然，这个具体的数字依赖于特定的飞行情况，但是哥哥肯定会比弟弟年轻这是一定的。

这个问题的争议点在哪呢？它争议就争议在：狭义相对论里有钟慢效应，也就是说运动的物体他的时间会变慢。那么似乎可以说哥哥离开地球在太空里运动了一圈，所以哥哥是运动的，那么哥哥的时间会变慢，回到地球更年轻好像说得通。但是，运动不是相对的么？你站在地球上觉得是哥哥在动，那么我站在飞船的角度来看，我也可以觉得是弟弟（包括整个地球）在远离我然后靠近我，那么运动的那个人就是弟弟，因此弟弟的时间更慢，兄弟见面的时候应该弟弟更年轻。这样不就前后矛盾了么？

双生子问题是一个佯谬，佯谬就是说它看起来是错的，是矛盾的，其实是正确的。也就是说，如果我们真的有这样一对双胞胎，哥哥去外面浪了一圈再回到地球，他是真的会更年轻。但是，这样的话，我们要如何解释后面那种矛盾的说法呢？也就是，站在飞船上哥哥的角度看来，运动的是弟弟和地球，为什么不可以认为弟弟和地球才是那个时间变慢的呢？

有人意识到是加速减速这个过程在作怪，但是加速减速他一样可以说，我在飞船上看，地球也是加速离我远去，再加速再回来。然后甚至有人说这里有加速度，就应该把广义相对论搬进来解释，在这条邪路上走地更远的甚至说：哥哥不是加速运动么？等效原理说加速度等效于引力，所以哥哥在加速的过程产生了引力，而广义相对论又说引力是时空弯曲，那么哥哥加速使得时空弯曲了。

其实，双生子佯谬不仅是让许多初学者疑惑，在相对论的几何语言普及之前，许多物理学家对它也是头疼不已。他们到了 20 世纪 50 年代还在吵这个，物理学家们吵就不是像我们这样在群里或者论坛里发表一下意见看法，他们是发文章到《自然》、《科学》这样的顶级学术杂志里吵，所以你可以想象一下那时的情况。但是，当几何语言普及之后，物理学界几乎就没人再因为这个争论了，因为在几何语言下，这个问题简直简单得不像话，它就跟 2+2=4 一样清晰简单，那还有什么好吵的。

为什么几何语言可以如此大幅度的降低双生子佯谬的难度呢？这里就涉及到了学习相对论里最重要的一个事：学习相对论最重要的就是要分清楚相对论里哪些东西是相对的，哪些是绝对的。你要是看这个理论的名字叫相对论，就认为什么都是相对的，那就完了。其实相反，狭义相对论的两个根基“光速不变”和“相对性原理”都是绝对的：前者说光速是绝对的，后者说物理定律的形式是绝对的，这其实是一个不折不扣的“绝对论”。

我们再回过来想一想，双生子佯谬到底为什么这么麻烦？不就是因为滥用相对，认为什么都可以相对，所以站在哥哥的立场和弟弟的立场应该都一样从而导致了佯谬么？那为什么我们用几何语言可以轻松把这个问题理清楚呢？因为我们在使用几何语言的时候，我们是把时 3 维空间和 1 维时间看做一个整体的 4 维时空。用 3 维眼光看世界，3 维空间和时间都是相对的，但是 4 维时空确是绝对的。当我们站在更高的维度（4 维时空）里看问题的时候，那些因为相对产生的各种问题就自然消失了。所以，使用几何语言思考相对论，是站在更高的维度上看问题，这是一种思维方式上的降维打击。看过刘慈欣《三体》的同学，想必都对降维打击产生的效果印象深刻，学习相对论，我们也要尽快提高自己的维度~

如果想体会一下 3 维语言处理双生子问题的复杂度，可以看看我之前写过的一篇《双生子佯谬过程全分析》，其处理问题之麻烦，逻辑之烧脑简直灭绝人性。虽然我已经尽量清晰通俗的语言来说这个问题了，但是读者的问题还是跟雪花一样飞过来。最开始我还比耐心的一个个在群里解释，后来就实在受不了了。要跟人把这个问题彻底解释清楚，少则一两个小时，多则一下午，太费时费精力了。而且，后面要理解许多人的问题都非常困难，因为要提出一个正确的相对论的问题也需要一定基础，有些同学相对论的基础知识不牢，提的问题都是问题，那还怎么去理解双生子佯谬呢？

这就像是游戏里刚出来就要去打终极 BOSS，下场自然可想而知，这也是我为什么现在就这么着急的来讲几何语言的一个原因：我实在不想再回答 3 维语言的双生子问题了。而且，把自己局限在这几个效应佯谬里，也不是什么好事，因为讲相对论的人虽然经常讲这个几个东西，但是这些东西绝非相对论的精髓，大家早点从这些框框里跳出去，去感受一下相对论里更精妙的东西才是好事。

14 双生子佯谬的几何解释

好，我们下面来看看从几何语言是如何降维解决双生子佯谬的问题的。我们先假设地球做惯性运动（忽略地球自转和引力场什么的），以地面系为基准系，我们在时空图里画一画哥哥和弟弟的世界线。

弟弟的世界线简单，因为他一直待在地球没动，所以他在空间坐标里没动，流逝的只有时间。那么，弟弟的世界线就是一条跟 t 轴平行的直线。

哥哥的世界线稍微复杂一点，但是也很容易。哥哥从地球出发，去太空浪了一圈再返回地球，这其中的过程无非是先加速远离地球（加速之后有没有匀速我们都不管了），太空里飞了一段时间要掉头返回地球，那么其中必定先减速，再反向加速驶向地球，最后还要减速降落在地球上。因为匀速运动的世界线是一条斜直线，那么加速运动的世界线就是曲线了，这曲线大致就是下面这个样子。

我们用 a 表示哥哥离开地球这个事件，b 表示哥哥返回地球跟弟弟见面这个事件，那么这个时空图就大致是下面这样的：

问题来了，时空图在这里，哥哥弟弟的世界线也都画出来了，那么如何从图中判断哥哥弟弟谁更年轻呢？时空图里纵轴是时间轴，单从时间轴来看，哥哥和弟弟的世界线在时间轴的投影刚好是一样长的，那么是不是这样就代表哥哥弟弟经历的时间是一样长的呢？如果他们经历的时间一样，那么重逢时哥哥弟弟的年龄就应该一样大啊，那怎么还会有双生子佯谬呢？这显然跟事实不符。

那么这个时间到底要怎么看呢？我们先来想一想，我们要判断地球重逢时谁更年轻，其实就是判断在事件 a 和事件 b 之间哥哥弟弟谁自己经历的时间更长，我这里特别强调是自己经历的时间，为什么要这样强调？在牛顿力学里，时间是绝对的，全世界的人都共用一个时间，因此这么说是多余的。但是在相对论里时间是相对的，不同参考系对时间的测量也是不一样的（正因如此洛伦兹变换里两个系的时间 t 和 t’是不相等的），那么在哪个参考系测量的时间可以表征一个人的真实年龄变化呢？或者换句话说，哪个时钟可以表征一个人年龄的真实变化呢？

答案显而易见：只有一直跟自己处于同一个参考系的时钟测量的时间才是自己年龄变化的真实时间。也就是说，只有我口袋里那块表的走时才是真正跟我的年龄增长对应的，我们把这个自己随身携带的时钟测量的时间称为固有时。相对论里时间是相对的，伦敦的那口大笨钟跟我不在一个参考系，凭什么说它的走时测量的是我的时间？

想通了这点，上面的事情就好理解了：我们把哥哥和弟弟的世界线都投影到时间轴，这其实得到的是地面系的时钟测量哥哥弟弟经历的时间，这钟相等没有任何意义。我们得用地面系的时钟测量弟弟的时间，再用飞船系的时钟（也就是哥哥随身带的时钟）测量哥哥经历的时间，也就是哥哥的固有时，这样对比才行。

那么问题来了：根据时空图和世界线，我们要如何得到哥哥的固有时呢？

15 世界线和固有时

在这里，我先给出这个极为重要的结论：世界线的线长等于固有时。

这句话很短，意思却很明确，他就是告诉我们时空图里那个粒子的世界线的线长就表征了粒子的固有时，也就是跟粒子一直保持相对静止的时钟测量的时间。在上面的双生子佯谬的时空图里，哥哥和弟弟的世界线都画出来了，那么我们可以求出他们的线长。现在你说世界线线长等于固有时，那我们要比较哥哥弟弟的固有时，直接比较他们的世界线线长就完了。

所以，如果我们知道上述结论，那么双生子佯谬这个问题就简化为比较哥哥和弟弟世界线的线长，谁的长一些谁经历的时间就多一些，那谁就更老，那问题就相当简单了。因此，现在问题的关键就是如何理解上面的结论：为什么在闵氏时空里世界线的线长会等于固有时呢？

这个事情我们可以这样理解：固有时是什么？固有时就是自己随身带的时钟测量的时间，说得再准确一点，那就是跟自己一直处在同一个参考系里的时钟测量的时间。因此，如果一个时钟始终跟你处在同一个参考系里，它自然觉得你一直是静止不动的。比如，在飞船里的哥哥虽然要经历加速减速运动，还可能在宇宙里各种浪，但是在飞船里的人和时钟看来，哥哥一直坐在那里没动。

那么，重点来了：时钟觉得你不动，其实是觉得你在空间里没动，也就是说觉得你在空间上的位移为零。那么，你在时空（时间 + 空间）里移动的间隔就将全部由你在时间上的间隔贡献（因为空间没动，间隔为 0）。

什么意思？我们再来理一下时空间隔这个概念：狭义相对论统一了时间和空间，用时空图上的一个点表示发生在某个时间某个空间上的一个事件，那么两个事件肯定就表示为时空图上的两个点，那么这两个点之间的距离（闵氏距离）就是这两个事件的时空间隔。而且，我们还反复强调了，闵氏几何里的时空间隔，就跟欧式几何里的空间间隔一样，它是不会随着参考系的变化而变化的。也就是说，只要发生了两个事件，那么不管我是在地面系看，还是在飞船系看，这两个事件信息虽然不一样，但是它们的时空间隔一定是一样的。

在欧式几何里，欧式线元是 dl²=dx²+dy²，所有在 x 轴上相隔 dx，y 轴上相隔 dy 的两个点的空间间隔，或者说空间距离也就是dl²=dx²+dy²。同样的道理，在闵氏几何里，闵氏线元是 ds²=-dt²+dx²，所以，在时间上和空间上分别相差 dt、dx 的两个事件，它们之间的时空间隔也就是 ds²=-dt²+dx²。

我们现在想知道固有时，也就是想知道跟自己处在同一个参考系里的时钟的走时。上面我们已经分析了，在自己所处的参考系里，肯定觉得自己是静止的，也就是空间间隔 dx=0。因为时空间隔是 ds²=-dt²+dx²，把 dx=0 代入进去我们就能得到ds²=-dt²。这就是在上面说的，自己参考系里的时空间隔全部由时间间隔贡献的意思。

有了ds²=-dt²，事情就明朗了：dt 就是在自己所在参考系里的时间流逝，而 ds 是时空间隔，也就是时空图上两点的距离。这个微分符号 d 就是在告诉我们这是两个间隔无穷小的事件，如果我们把许多无穷小的这种事件累积起来（也就是对ds²=-dt²做积分运算），那么 dt 累积起来就是时钟流逝的时间，也就是固有时；而把 ds 累积起来，也就是把所有相邻时空点之间的距离累积起来，那得到的就是时空图里这条世界线的长度。

这就无可辩驳的向我们证明了：世界线的长度等于固有时。

其实，只要我们理解自己相对于自己所在的参考系肯定在空间上是静止的，所以时空间隔全部由时间间隔贡献。而时空间隔就是时空图里两点的距离，这个距离累积起来就是世界线的长度，而时间间隔累积起来自然就是这个参考系里流逝的时间就行了。上面做的各种简单的计算，无非就是从数学上更加严格地证明了这一点而已。

想通了这点就会觉得其实“世界线长等于固有时”是很正常的事情，在一些相对论的教材里，他们甚至直接拿这个来定义标准钟的。也就是说，他们在教材不会向你解释为什么“世界线长等于固有时”，而是直接告诉你“只有世界线的线长等于固有时的钟才是标准钟”，才是准确的钟，否则你的钟是有问题的。可见，在大家眼里，这个结论实在是非常自然的。

16 双生子佯谬之完结篇

好了，如果我们能够理解“世界线的线长等于固有时”，那么困扰大家多年的双生子佯谬就瞬间变成了一个极其简单的问题。我们再来看看双生子佯谬的时空图：

比较哥哥弟弟重逢时谁的年龄更大，就是比较他们两个的固有时，就是比较哥哥和弟弟世界线的线长。那么，他们两个的世界线谁的更长一些呢？

其实这根本都不用定量的去计算，一眼就能看出弟弟的世界线更长，因为闵氏几何里线段长度是时间和空间项的平方相减之后再开方得到的。这个求线段距离的公式我们前面也说了，其实就是闵氏线元稍微处理一下，如下图：

所以，如果两条线在时间轴上长度一样（比如哥哥和弟弟的时间都是从 a 到 b），那么在空间上走的越多的它的总线长就越短。弟弟静止没动，他的世界线是完全平行于 t 轴的，在 x 轴上都没有任何分量，也就是Δx=0，所以他的世界线肯定是最长的。哥哥因为去太空飞了一圈，所以空间上的分量Δx>0，那最终得到的 S 的值肯定就比弟弟更小了。

我们可以想象一个最极端的情况，我们假设哥哥以光速运动，那么它在空间上走的距离就最大。而我们知道光子的世界线长度为 0，所以这时候哥哥的世界线长度就是最小值 0 了，0 肯定比弟弟的世界线长度更小吧。

如果大家对这种粗略的讨论不放心，我们可以换种更精确的方式讨论。如下图，我们把弟弟和哥哥的世界线用很多平行于 x 轴的虚线分隔开，如果我们的分割线足够多，那么在每一个小段里哥哥的世界线就可以近似看做一条斜直线，而它的线长是显然比弟弟世界线里的那一小段短的（这我们在上面已经给过结论了）。由于每一小段里哥哥的世界线都更短，那么累加起来的总世界线肯定还是更短了。

总之，大家如果理解闵氏时空的线长计算公式，我相信理解哥哥的世界线更短是非常容易的，而世界线更短就意味着自己经历的时间（固有时）更短，那么重逢时哥哥就更年轻。这样，双生子佯谬就是很明显的事情了。

于是乎，我们发现让我们头疼不已的双生子佯谬就这样被解决了。在几何语言里，复杂的双生子问题被简化到仅仅比较一下哥哥弟弟两条世界线的线长就行了，而只要我们理解在闵氏几何里计算线长要用闵氏几何的方式（ds²=-dt²+dx²）去度量就没什么问题了。其实，你也不用觉得奇怪，把代数问题几何化之后带来问题难度的大幅度降低并不是什么奇怪的事情，我们在初中高中的数学里，不也经常借助画图去理解函数、方程的性质么？

这样处理问题简单是简单了，但是细心的人还是会有疑虑，他觉得：虽然你在这个以地面为基准系的时空图里确实严格地证明了哥哥的世界线更短，所以回来的时候更年轻。但是我如果不以地面系为基准系呢？我在其他的参考系里来看，来画时空图，比如我要是站在哥哥飞船的视角来画时空图，那结果会不会又不一样呢？因为说到底，大家觉得双生子佯谬难以理解，就是因为你可以站在弟弟的角度，也可以站在哥哥的角度，这样一相对就没完没了了。

这在以前的思维里确实是大问题，但是，在几何语言里这确不是问题。为什么呢？因为线长是一个几何量，这种几何量是不会随着坐标系的变化而变化的（因为它们是根据线元定义的，而线元在不同的坐标系里都是一样的），也就是跟坐标系的选择无关。这一点我们在二维欧式几何里也可以非常清楚地感觉到：你在二维欧式平面里有一条线段，那么这条线段的长度就是固定的。不管你是上下左右的移动这个直角坐标系，还是顺时针逆时针旋转这个直角坐标系，线段的长度始终都是一样的，这一点相信大家不难理解。

那么，同样的，在闵氏几何里，不论你选择哪个惯性系作为基准系，一条世界线的线长都是一样的。也就是说只要哥哥的世界线在一个参考系里比弟弟的世界线短，那么再所有的惯性参考系里都比弟弟的世界线短。这就跟在欧式几何里一根木棒只要在一个直角坐标系里比另一根木棒长，它在所有的直角坐标系里都比那根木棒长一样的道理。

其实，我们再仔细想一下，当初我们为什么选择闵氏几何来描述狭义相对论？不就是因为我们发现了在洛伦兹变换下，也就是在惯性参考系之间不论怎么相互转换，ds²=-dt²+dx²作为一个整体它的值是不变的么？然后我们以 ds²=-dt²+dx²为线元建立了闵氏几何，而在闵氏几何里曲线的长度就是根据这个线元来定义的。所以，世界线的长度在闵氏几何不同的参考系里肯定就是一样的，我们也压根没必要舍近求远，去选择更复杂的参考系给自己找不痛快。

这样，我们就能消除那个疑惑，放心大胆的说哥哥的世界线更短了。于是，用闵氏几何讨论双生子佯谬的问题就全部结束了。其实，只要把几个关键的弯转过来，你就会发现双生子佯谬其实是非常简单的一个问题，它完全不值得我们花费那么多的时间精力在这里绕来绕去（这个问题跟薛定谔的猫在社群里并称两大月经问题），但是不使用几何语言，这好像也是没办法的事，太复杂了。相对论还有非常多精彩的东西等着我们去探索发现，在双生子这棵小树上把自己吊死了岂不可惜？闵氏几何虽然看上去有点怪异，但是当我们顺着思路慢慢看的时候，就会发现它其实也没那么奇怪，它不过就是在欧式线元的前面加了一个负号而已，其他的逻辑跟欧式几何都几乎是一模一样的。

17 结语

文章到这就先告一段落，能够坚持看到这里的那妥妥的都是真爱了。我写这篇文章主要是想让更多人了解闵氏几何，了解闵氏几何是如何处理狭义相对论里的问题的，最好是让读者能开始习惯用几何语言讨论相对论问题。

所以我不能直接给你下定义，然后告诉你如何用闵氏几何处理这个那个问题，因为这样很多人会不服气，凭什么相对论的问题可以转化成这样的几何问题？为什么闵氏几何里的这个就对应了相对论里的那个问题？因为闵氏几何并没有那么直观，你把狭义相对论翻译到闵氏几何并不像我们把一个图形画到黑板上那么显而易见，所以我必须先把自己的知识清空，从头从零一点点的开始讲，让大家自然的切换到闵氏几何中来。于是，文章就不可避免的长了起来。

另一方面，我这只是科普性质的文章，重点是想让大家了解闵氏几何处理狭义相对论问题的核心思想，因此，我不会像教科书一样把各个概念和术语都写出来。相反，为了降低大家理解的难度，能不用术语的地方我尽量不用术语，能不写公式的地方尽量不写公式，我这真的只是一个闵氏几何的入门篇。大家如果想更全面深入的了解相关内容，可以去找专业的闵氏几何和相对论的教材，这里我还是推荐北京师范大学梁灿彬老师的《从零学相对论》（入门篇）和《微分几何入门与广义相对论》（高级篇），需要这两本书的电子版和配套教学视频的，可以在后台回复“梁灿彬”或者“梁老师”。把我这篇文章看懂了，再去看《从零学相对论》应该会很容易，更深入的问题我们后面再说。

最后，长尾君希望大家能和闵氏几何搞好关系，毕竟后面还有更多更精彩的话题都指着它呢~

更新：

根据这两天读者的反馈，看来还有两个地方是大家比较困惑的：

1、为什么博尔特那里还是减去光速 c 乘以博尔特的时间，而不是乘以博尔特的速度？而且为什么从火车系去看，博尔特的那个Δs 的值依然不变？

答：狭义相对论的几何语言的核心就是：三维欧式空间里Δx²+Δy²+Δz²不随坐标系的变化而变化（Δx²+Δy²+Δz²=Δx’²+Δy’²+Δz’²），所以我们在闵氏几何里也构造了一个Δs²=Δx²+Δy²+Δz²-(cΔt)²，让这个量是不随坐标系变化而变化的（Δx²+Δy²+Δz²-(cΔt)²=Δx’²+Δy’²+Δz’²-(cΔt’)²），对于光这个值刚好等于 0，这个刚好对应了光速不变而已。这个Δs 是我们自己构造出来的一个东西，叫做时空间隔，它的目的就是要找到这样一个东西，让他类似于三维空间里的长度不随坐标系的变化而变化，所以当这个由光变成博尔特的时候，依然还是光速 c 乘以时间，因为Δs 的形式就是这样的。

为什么博尔特的Δs 不会随着参考系的变化而变化，这个通过洛伦兹变换可以很容易证明Δx²+Δy²+Δz²-(cΔt)²=Δx’²+Δy’²+Δz’²-(cΔt’)²，我们现在只是用几何语言来诠释这个东西，来寻找这个等式后面的几何意义。

2、最核心的，双生子佯谬那里，为什么不能是站在哥哥的角度，是弟弟和地球远离地球，再回来与哥哥重逢呢？这样运动的就是弟弟，变老的就是弟弟啊。

答：看来大家这里还是没看太明白，其实这点我在文章里花了很大篇幅特地解释了，在 16 节的后半部分～

如果从代数语言来说，惯性运动和非惯性运动之间的区别是绝对的。举个例子，你在加速的汽车上，你会感觉到椅子的推背感，减速的时候身体会前倾，减速太快你可能会撞到前面去，这种体验在家里静止的人是没有的。所以这两种参考系之间的区分是绝对的，你在加速的车上和在家里静止的人的区别是绝对的，这无法通过相对而消除。你不管以谁为参考系，只有在车上加速减速的人会感觉到推背感和身体前倾。

而我在文章里是通过几何语言来区分，从几何语言来看，世界线（作为一连串事件的集合）是绝对的。在闵氏时空里，世界线的长度就跟欧氏几何里一根线段的长度一样，因此它的长度是不会随着参考系的变化而变化的。所以，哥哥的世界线只要在一个参考系里比弟弟的短，那么在所有的参考系里都比它短，我们没必要再给自己找麻烦选择负责的参考系。这是几何语言的核心，抓住那些不随参考系变化而变的量~

再更新：

还有一些朋友对尺缩效应的那个图有疑问，原因各种各样。下面这张图是梁灿彬老师《从零学相对论》里关于尺缩效应的解释，相信不管你是出于什么原因，看了这个应该能明白了。

相关回答：

如何深入浅出地讲解麦克斯韦方程组？7303 赞同 · 358 评论回答怎么解释麦克斯韦方程和牛顿力学的不兼容性?8841 赞同 · 326 评论回答微积分到底是什么?3 万赞同 · 1739 评论回答杨振宁的成就很伟大吗？2.4 万赞同 · 1089 评论回答如何学好高中物理？196 赞同 · 62 评论回答

【长尾科普系列】已出版 4 本书：

事实上我们所知道的食草动物，几乎没有一种是单纯的素食主义者。

路透社曾报道过印度的一头牛，在一个月之内吃掉了 48 只小鸡。

鹿会吃掉受伤后无法飞走的小鸟，还被人拍到食用野兔的尸体。

家兔吃肉对养过兔子的人来说并不新鲜。加拿大的白靴兔也被发现吃鸟，甚至其他兔子和猞猁的尸体。松鼠也会吃肉，不管是死掉的老鼠、还是一只鸟，它们都不介意。

河马一夜能吃掉 40 公斤草，但是偶尔也会吃黑斑羚、幼年非洲象，甚至同类的尸体。现在它们已经被食草动物除名，成了杂食动物。大象会利用自己灵活鼻子捞鱼吃。

长颈鹿爱好捕食者吃剩的骨头。这种现象还有个专有名词，叫做嗜骨癖（osteophagia）。

草食性哺乳动物吃肉并非特殊个案。在摄像机的帮助下，从圈养到野生，从热带草原到北极圈，到处都能发现这种现象。

一种解释认为，食草动物吃肉就和吃土、吃毛一样，是一种异食癖。在缺乏蛋白质或某些矿物质，或者有寄生虫时，它们就会以吃肉代替吃植物。

不过，许多在人工喂养下，没有明显疾病的食草动物也会对肉表现出兴趣。这说明食草动物吃肉不见得是病理性的行为。

首先，食草动物也能消化动物蛋白和脂肪。对于它们而言，动物是比植物更高效的营养成来源，不但能量密度更高，而且脊椎动物并不能直接利用植被中的纤维素和木质素等，需要靠肠道菌群才能分解消化。

所以，牛羊和猪的饲料中经常添加 5%以下的“动物性饲料”，比如牛奶、肉粉、肉骨粉、鱼粉。曾经流行一时的疯牛病，就是牛饲料中的肉骨粉导致的。

给你的宠物兔喂排骨同样是不明智的。它们代谢动物脂肪的能力不强，长此以往会导致肥胖等问题。

其次，所谓的“吃肉”“吃素”主要是为了分类方便，它们的分类界限并没有那么明显，绝对的肉食动物和植食性动物都是极少数。

比如盛产草食性哺乳动物的偶蹄目（鲸偶蹄目），也包括各种杂食和肉食动物。

早已灭绝的偶蹄目动物蒙古安氏兽（Andrewsarchus mongoliensis），根据骨骼推测也是一种食肉或食腐动物。

鹿的祖先古鼷鹿（Dorcatherium）和一些现代鼷鹿也被认为是杂食动物。它们吃昆虫、水生动物和腐肉。

回到食草动物为什么要吃肉的问题上，其实正确的问题应该是：为什么它们要吃草？

在一个陆生生态系统中，能量沿着食物链流动：首先，植物通过光合作用，固定太阳提供的光能。其次，食草动物通过吃植物，获取自己所需的能量。最后，食肉动物又从食草动物的肉中获取能量。

考虑到食物链每级的能量转化效率不超过 10%，一个生态系统能承担的食肉动物的数目非常有限。而供养一群肉食者，就需要相当庞大的能量消耗。

以人类为例，世界上约有 70 亿人，同时养着 650 亿只鸡、8 亿头猪、10 亿头牛、20 亿头羊。它们生产的肉、蛋、奶依然不够所有人食用。

这决定了肉食性的动物只能是少数，大多数动物必须以素食为生。

然而，这并不能阻止广大食草动物们对偶尔开荤的向往。

食草动物才不是吃素的 https://www.zhihu.com/video/1116367988017696768

第一反应是：恙虫病（一种急性传染病）

对于恙虫病患者，如果没有早期诊断并及时应用有效的抗生素进行治疗，预后比较差，特别是老年人、孕妇和有并发症者，部分病情严重者可因多器官功能衰竭、肺或消化道大出血而死亡（病死率各地报道不一，未用抗生素病死率 9％-60％）。

不过，恙虫病一旦早期确诊，及时进行病原治疗，绝大部分预后良好。

病原治疗主要是应用氯霉素、四环素（儿童慎用）或者红霉素，效果都很好，一般用药 3 天内体温可恢复正常，另外，多西环素、罗红霉素、阿奇霉素或诺氟沙星等抗生素对恙虫病也有疗效。我在呼吸科轮转时，带教老师碰到恙虫病患者，一般用多西环素，效果也是杠杠的！

（注意：青霉素类、头孢菌素类和氨基糖苷类抗生素对恙虫病没有治疗作用）

重点来了↓↓↓

如何早期发现可疑恙虫病：

如果突然出现发热，1~2 天内体温迅速升至 39~41℃，伴有头痛、疲乏等症状，首先肯定要及时到正规医院就诊。如果发病前 3 周内有接触丛林、草地等，应注意寻找身上有无焦痂或溃疡（尤其是腋窝、外生殖器、腹股沟、会阴、肛周、腰背等处），有的话请务必主动告诉医生，因为这是诊断恙虫病的一条重要线索。（当然，医生通过了解病史和详细查体后并不难确诊，不过早点确诊总是有利无弊的）

以下详细展开（便于理解上面那段话）：

• 恙虫病的流行病学特征：

1）主要传染源：鼠类。

2）传播途径：恙螨为其传播媒介，通过恙螨幼虫叮咬传播给人。

3）人群易感性：人对本病普遍易感（不分男女老幼），不过从事野外劳动、较多接触丛林杂草的青壮年发病率较高。（恙虫病患者在发病前 3 周内一般有户外工作、露天野营或在林地草丛上坐、卧等。）

4）流行特征：我国南方多发于夏秋季，见于 5~11 月，6~8 月为高峰；北方省份多发于秋冬季，以 9~12 月为多，高峰出现在 10 月。本病多分布于热带及亚热带的河溪两岸，且多见于灌木、杂草丛生的平坦地带，以海岛、沿海地区较多见，山区较少。

• 恙虫病的临床表现：

起病急，体温迅速上升，1~2 天内达 39℃~41℃，持续 1~3 周，伴有寒战、剧烈头痛、全身酸痛、疲乏、嗜睡、食欲下降、恶心呕吐等，体征可有眼结膜充血、颜面及颈胸部潮红，皮肤出现焦痂或溃疡、皮疹，另外可有肝淋巴结肿大、脾肿大等。病程进入第 2 周后，病情常加重，出现各种并发症，可表现为心慌、咳嗽、气促、胸痛、神情淡漠、烦躁，甚至抽搐或昏迷，少数患者会出现鼻出血、胃肠道出血等^[1]。

上述临床表现中，有一个最具有特征性的体征：焦痂和溃疡（可见于 70％~100％的患者）。

恙螨幼虫叮咬人体后，局部出现丘疹，继成水疱，随后结成黑色痂皮，形成焦痂，焦痂呈圆形或椭圆形，直径 2~15mm，多为 4~10mm，边缘突起，周围有红晕，若无继发感染，则不痛不痒，也无渗液。痂皮脱落后变成溃疡，基底部为淡红色肉芽创面。焦痂可见于体表任何部位，但由于恙螨幼虫喜好叮咬人体湿润、气味较浓以及被压迫的部位，故焦痂多见于腋窝、外生殖器、腹股沟、会阴、肛周和腰背等处^[1]。

之前在呼吸科还遇到过一例出现在腹部的焦痂，如下图所示：

最后提一下恙虫病的预防：

由于目前尚无针对恙虫病有效的疫苗，因此，预防的关键在于灭鼠、灭恙螨和做好个体防护措施。其中，个体防护措施包括：

流行季节在野外施工、生产、行军、野营、训练时，应扎紧袖口、裤管口，把衬衣扎入裤腰内;不要在草地坐卧;避免在草丛、树枝上晾晒衣服和被褥。在流行较重地区，有条件时可使用药物预防。身体外露部分，如手、颈、耳后以及小腿等处可涂擦避蚊油(邻苯二甲酸二甲酯，dimethyl phthalate )，有 2h 的防护作用，或避蚊胺(deet )，有 4h 的防护作用，但涉水后均失效，而以邻苯二甲酸二甲酯 70%与邻苯二甲酸二丁酯( dibutyl phthalate ) 30%合剂涂擦，可延长防护作用至 8h，经过 3~4 次涉水，仍有一定的效力。衣服可用邻苯二甲酸二丁酯乳剂(以 0. 5 %肥皂水作乳化剂)浸泡衣服(包括袜子)，每套约 670ml，浸泡的衣服水洗 5 次后仍有一定的防护作用。据报道，恙瞒在人体皮肤上爬行 20 一 30 min 以至 1h，多尚未叮咬。因此，野外作业后，及时换衣、洗澡或擦澡，重点擦洗腋窝、腰部、会阴等皮肤柔软部位，可减少被恙满叮咬的机会^[2]。

这个问题有点意思，这个问题的解答涉及到几个方面，包括导线的发热理论和散热动态平衡方程式，还有电压损耗理论，以及短路理论。我们这就开始讨论。

我们先看看百度怎么说：

远距离输电要用高压的原因是：在同输电功率的情况下，根据公式 P=UI，要使输电电流 I 减小，而输送功率 P 不变（足够大），就必须提高输电电压 U。电压越高电流就越小，这样高压输电就能减少输电时的电流，从而降低因电流产生的热损耗和降低远距离输电的材料成本。

由焦耳定律 Q=I^2Rt，减小发热 Q 有以下三种方法：一是减小输电时间 t，二是减小输电线电阻 R，三是减小输电电流 I。可以看出，第三种办法是很有效的：电流减小一半，损失的电能就降为原来的四分之一。要减小电能的损失，必须减小输电电流。

百度的说法属于经典表述，但这种表述对吗？我们来分析一下：

我们设导线的电阻是 R，当经过时间 t 后，导线产生的焦耳热量 Q 为：

，式 1

从式 1 看，增大电流 I 或者增高电压 U，对于导线产生的焦耳热来说，似乎是一致的。我们看到，电压增加一倍，或者电流增加一倍，导线的焦耳发热量均增加四倍。不管是电压也好，是电流也好，并没有本质区别。

这正是题主的疑问之所在。

这里先打一个伏笔，就是电压 U 到底指的是什么电压。往下看就明白了。

我们知道，焦耳发热的热量作用在导线上，导线会产生两种作用：其一是导线温度升高，引起了热量的消耗；其二是导线向空间中散发热量，同样也引起热量的消耗。这两种热量消耗与产热之间存在热平衡关系。

我们设导线温度升高消耗的热量是 Q1，导线散热消耗的热量是 Q2，则有：

，式 2

式 2 叫做导线的热量动态平衡方程式。其中的 Q1，它等于导线材料的比热容 c 与导线质量 m 的乘积，再乘以导线的温度升高值Δθ，Δθ等于导线当前的温度θ与先前的温度θ0 之差，即：

。

我们容易想到，导线持续输送电能时，经过一段时间，导线的温度必然会恒定，也即Δθ等于零。如此一来，Q1 等于零。

我们再看式 2 中的 Q2，它与综合散热系数 Kt 与导线的表面面积 A，还有导线的表面温度与环境温度差τ的乘积有关，即：

。

我们由式 2 可知，当导线的表面温度稳定后，

。我们把 Q 的电压表达式和电流表达式代入，得到：

电流表达式：

，式 3

我们知道，电阻

，这里的ρ是电阻率，α是电阻温度系数，L 是导体长度，S 是导体截面积，θ是导体表面温度。再注意到导体表面积 A，我们忽略掉导体的两个端面，于是导体表面积

，这里的 M 是导体截面周长，L 是导体长度。我们把这些都代入到式 3 中，得到温升的电流表达式：

，式 4

从式 4 中我们看到，导体温升与电流的平方成正比，与导体的截面积 S 成反比，与导体截面周长也成反比。特别注意的是：温升与导线长度 L 无关！由此可知，导线的载流量与导线长度无关！

我们再看温升的电压表达式：

，式 5

从式 5 中我们看到，温升与导线单位长度的电压降“U/L”的平方成正比。

前面的伏笔在此揭开了，原来式 1 中的电压其实就是导线单位长度的电压降。

我们来做一个段落总结：

当通电导线经过一段稳定时间后，它的温度已经稳定，此时导线的稳态损耗体现在导体相对环境温度的温升上。由式 4 和式 5 可以看出，温升与电流的平方成正比，与导线单位长度电压降的平方成正比。

可见，百度的说法是需要补充纠正的。

特别提醒：我们由

和

，可以推出

。这个式子用一位著名科学家来命名的，叫做牛顿散热公式。这个式子是牛顿首先提出，并用在他的理论中。

从以上讨论中，我们隐隐约约地感觉到，输电的损耗问题不但与温升有关，还与电压损耗有关。

翻开《工业与民用配电设计手册》第四版，在第九章我们能看到有关输电线路的电压损耗表达式：

，式 6

式 6 中，Δu%是线路电压损失百分数，Un 是输送电的标称线电压，R0 是三相线路单位长度的电阻，X0 是三相线路单位长度的感抗，cosφ是功率因数，I 是线路电流，L 是线路长度。

提醒一下：式 6 不是超长距离输电线路的电压损耗。如果一定要给出超长距离的电压损耗，则必须考虑电磁场的许多效应。由此可见，这里面的知识量非常丰富。具体可见有关输配电和工业电磁场方面的书籍，此处不给予详细讨论。

我们从式 6 中看到，电压损失与导线和线路中流过的电流成正比。由此可以想到：如果把电压提高，把电流减小，那么就能减少线路中的电压损耗。

我们看下图：

从图 2 中，我们就能看到电压损失的情况。

我们看到，发电机所发的电压必须高于额定电压 5%，而升压变压器 T1 的副边电压高于输送电线路额定电压 10%。由于电压损失的原因，到达降压变压器 T2 的原边，电压已经降低到等于额定电压 Un。在降压变压器 T2 的副边，同样需要把电压提升到高于副边线路额定电压的 5%。

图 2 反映了在实际运行中，为了确保用电设备的电压符合标称电压要求，配电系统采取的电压调整措施。

现在，我们再看看当配电网发生短路时，导线的受力情况。

当发生短路时，短路电流很大，导线之间的短路电动力 F 可以采用毕奥.萨法尔定律来分析，如下：

，式 7

式 7 中的 L 是导线长度，d 是导线间距，Kc 是导线的截面系数，I 是短路电流。

我们通过一个实例来看看短路电动力的大小：

设被考察的导线长度 L 是 100 米，导线间距是 d 是 1 米，导线的截面系数 Kc=1，短路电流是 100kA。把这些值代入到式 7 中，看看结果是什么：

我们看到，这 100 米的导线所受到的短路电动力是 20408kgf，差不多相当于 20.4 吨的力！可见，支撑这些导线或者架空线的铁架该要有多结实。当然，线路保护也必须快速动作才行。

这么大的短路电动力，和电压有关吗？用网络语言来说就是：式 7 与电压有毛关系。

在实际三相配电网中，当发生短路时，由于三相交流电相序的原因，A 相和 C 相配电线路受到的短路电动力是 2.65F，而中间 B 相配电线路受到的短路电动力为 2.8F。

当发生短路时，电压会发生何种变化？我们看下图：

图 3 中，我们设电源电动势是 E，线路电阻和电源内阻的合并电阻是 r+Rx，短路点的等效电阻是 Rk，则短路点的电压 U 为：

为了确保供电电压的稳定性，一般地，线路电阻（阻抗）必须小于短路点电阻（阻抗）的 1/50。我们不妨设(r+Rx)=Rk/50，代入到上式中，得到：

，式 8

原来，短路前后电压基本不变！我们把满足这种关系的配电网叫做无限大容量配电网。

我们周围的高压配电网都是无限大容量配电网，只有低压 220V/380V 配电网是有限容量配电网。尽管如此，由于短路时间很短暂，低压配电网在短路瞬间依然满足无限大容量配电网的特性。

我们看下图，此图是发生短路时的电压波形和电流波形，是我用 CAD 绘制的：

图 4 中，在时刻 0 的左侧，我们看到了正常的电压 u 波形和电流 i 波形。当在时刻 0 发生短路时，电流剧烈地增大到冲击短路电流峰值。之后，随着过渡过程的继续，短路电流成为到稳态值 ik。

此时的电压有何变化？从图 4 中看到，电压 U 基本不变。

可见，从配电网短路故障情况看，不管是短路电动力冲击作用也好，是短路热冲击作用也好，均与电压无关。所以，在配电网中，我们尽量提高电压减小电流，以减小故障电流的冲击。

总结一下：

1）线路损耗与电流的平方成正比，与配电线路单位长度的电压降的平方成正比。

2）降低电流提高电压，能有效地减小线路损耗，提高电网传输电能的能力。

3）提高电压，减小电流，能减轻配电网发生故障时的冲击效应，提高设备承受短路故障冲击的能力。

以上就是给题主的问题最终答案。

===================

晚上看了若干篇评论，似乎以中学生为主，而且纠结于最开头的式 1，后面的内容没人讨论。

其实，这篇文档的涉及到的知识远超中学生的认知能力。对于中学生来说，的确，能看懂前面的式 1 就不错了。后面的内容，中学生们应当看不懂才对，这从评论中就能明确地看出来。

这篇文档对配电线路导线的发热做了讨论，并导出温升与电流的关系，以及温升与单位长度导线压降的关系。我们看到，从温升作用看，两者是等同的。

然而，从配电线路的电压损耗来看，它与电流密切相关，所以减小电流，就能降低电压损耗。

特别重要的是，从短路电流对配电网的冲击看，电流居于主导地位，而电压的作用却十分有限。由此可知，从配电网的稳定性来看，减小电流具有很大的实际意义。

主要就是这些。

从法律角度讲一个吧。算不上逆天，只是觉得应该有。

云梦睡虎地秦简。

上过中国法制史的同学，肯定学到过关于它的介绍。

1975 年 12 月出土于中国湖北省云梦县城关睡虎地。墓穴里是一个秦朝名叫“喜”的基层官吏，喜有多热爱自己的工作呢？陪伴他下葬的不是常见的青铜器、金器、玉器，而是他工作时的秦简。可以见下图的样子。

见多了墓穴里的金银玉器，但从来没见过有人会把自己工作的竹简放进去。尽管位卑言轻，但他一定非常自豪满足于自己的工作。尽管这一生没有什么轰轰烈烈的成就，但无愧于自己的工作，无愧于这些竹简。对这位基层工作人员肃然起敬。

云梦秦简的珍贵之处有很多，这里仅仅列举几个和法律有关的。

1、世界上最早的法医记录

云梦睡虎地秦墓竹简上记载了缢死、流产、外伤检验等且还规定了检验缢死者的方法。这是世界上迄今发现最早的法医记录。

给后世的《洗冤集录》算是开了一个好头吧。

2、世界上最早的刑事侦查书籍

云梦睡虎地秦墓竹简《封诊式》是世界上最早的刑事侦查书籍。《封诊式》是关于查封与勘验程序式的一部书籍，共 25 节，3000 余字，书中大部分内容均以案例为主，以文书格式出现，具体有审讯、犯人、抓捕、自首、惩办、勘验等方面内容。

从这个角度来看，《封诊式》还颇有点英美法系判例法的味道。一课一例，有利于理解吸收。

3、世界上最早环保法

《田律》是迄今世界上最早的保护环境法律条文。《田律》以法律的形式规定保护环境的条款，规定：早春二月，不许到山林中砍伐树木；不到夏季七月，不许烧草以及采摘刚发芽的植物；不许捕捉幼鸟幼兽，不能毒杀水生动物，也不能用陷阱或网捕捉野生动物及鸟类。

用国家宝藏的一句话总结下：

守护国宝，守护律法初心。

感谢大家的点赞和评论~ 评论区发现许多超赞的回复，摘录部分如下：

@风雪夜归：我觉得自豪的是 2000 年了我们还能看懂它

@围城牛牛：1975 年，在湖北省云梦湖发现了秦朝时期的陵墓，出土了一些珍贵的竹简。这是一个重要的文物。其上面详述了秦朝法律文件，它共有 1,155 个竹简，近 4 万字。而这部秦简也详细记录了但是关于军队方面的惩处规则。其中有一段话是这么说的：朝廷征兵，如果没有什么特殊情况而延误行程的罚二副铠甲，晚到 3-5 天的应受斥责，晚到 6-10 天罚一个盾牌，超过 10 天者罚一副铠甲。但是若是下雨、大雪等自然原因的是不受到惩罚。也就是说陈胜吴广那种情况 ，不一定要同伴们一起受刑或者受死，起义的原因有可能是陈吴两人编的一个借口 。

@圞麟：所以，那些说考古是盗墓的能闭嘴了嘛？要是盗墓，这些无价的竹简能剩下吗

@方如：想象了一下，等我寿终正寝的时候，骨灰盒旁堆满了卷宗复印件……[调皮]

既然说到了秦简，那就再介绍一件文物，里耶秦简。

里耶秦简出土于湖南省湘西土家族苗族自治州龙山县里耶镇里耶古城 1 号井，共 37000 多枚，年代为秦王政二十五年(公元前 222 年)至秦二世元年(公元前 209 年)。

和云梦秦简不同，里耶秦简没有系统的法律条文，更多的是一个县城的档案记载。但是这份记载却相当地详实，像一部秦朝郡县生活的百科全书，写满了当时的各个方面，涵盖了秦朝职官设置、签署公文、人口管理、经济管理、司法管理、物资管理、官吏考核、监督问责、公文收发与传递等等。

另外，里耶秦简里还有迄今为止发现的最早、最完整的乘法口诀表实物“九九乘法表”，也就是说两千多年前，九九乘法表已经得到广泛应用了。

但是，要知道里耶位于湘西山地，即使是现在去里耶，交通也并不发达，在秦朝更是一个楚国旧地的南荒深山小县，而秦朝居然有如此严密完整的行政制度和方案，不愧是法家的奉行者。

“里耶秦简，用近 20 万个字，为我们描绘了 37000 多个从前。这如同复活了秦朝的一个细胞。继而复活了一个时代的生命气息。那时的小吏与平民，仍存于尺牍，可以阅读，可以理解，可以想象，可以在尺牍之间看到那些被秦时明月闪耀过的生命与时光。​​​”该段摘自《如果国宝会说话》的解说词。

事实上，周天子是建立了军队的，而且不止一支，而是两支军队，这两支军队一度非常强大。

在西周的大部分时间里，周天子都掌握着两支可能是当时的天下最强悍的部队，西六师和殷八师。这两只部队的兴衰和西周的国运休戚相关。

其中，西六师的驻地在周的发祥地——关中平原，并很可能在伐纣之前已经完成了编制，成为武王伐纣的主要力量，在《逸周书·世俘》中有：

“太公望命御方来，丁卯至，告以馘俘……吕他命伐越、戏、方，壬申荒新至，告以馘俘。。侯来命伐，靡集于陈。辛巳，至，告以馘俘。甲申，百唶以虎贲誓命伐卫，告以亳俘。……庚子，陈本命，伐磨百韦，命伐宣方、新荒，命伐蜀。……百谓至，告以禽宣方，禽御三十两，告以馘俘百韦，命伐厉，告以馘俘。……”

在本段中，在武王成功攻克沫（朝歌）之后，又命令太公望、、吕他、侯来、百唶、陈本、百谓六人各率军攻击殷的方国，这六人可能就率领了一师，合计六师。

而在武王殁后，成王即位，周公旦摄政，平定三监之乱，又东征奄、嬴等殷商与国。可能正是这次国家危机让周公旦及周天子对感受到了在广大的关东国土建立军事力量的急迫性。至少在康王世，一支新的军队建立起来，这支军队由 8 个师组成，称八师，由于驻地在东土，所以可成为“东八师”，或者根据其主要的军事驻地——殷商故土而成为“殷八师”。

在康王时代，殷八师已经开始活跃：

【虘又】東夷大反。白懋父以殷八师征東夷。唯十又一月。遣自 X 师征东夷。伐海眉。于厥復歸才牧师。白懋父承王令。易师率征自五颙貝。小臣逨蔑历。众易貝。用乍寶尊彝。——小臣逨簋

在小臣逨簋中提到，某年十一月，东夷反叛，伯懋父率领殷八师征伐东夷，兵锋直指海边（鲁北），胜利回师之后驻军牧师，赏赐功臣。

在本器中已经明确提到东征主力位殷八师。而战斗的指挥者伯懋父就是大名鼎鼎的卫康伯王孙牟。另外，此器中提到的牧师，正是牧野，也就是武王克商之战的主战场，看来在殷八师建立之后，位于今天河南淇县和浚县的牧野依然是重要的军事据点。

按照目前所知的金文铭文，西六师和殷八师应该是拥有土地和血缘结构，平时务农，在天子征召时挂甲上阵类似“军屯”的组织单位。过去常常有人怀疑这一点，认为这两支军队并非兵农结合的组织结构，针对这一点我们可以举出这样一件青铜器：

唯八月初吉。王各于周廟。穆公又盠立于中廷。北鄉。王册令尹。易盠赤巿。幽亢。攸勒。曰。用司六师。王行參有师。司土。司馬。司工。王令盠曰。赞司六师众八师艺术。盠拜稽首。敢對揚王休。用乍朕文且益公寶尊彝。盠曰。天子不叚不其。萬年保我萬邦。盠敢拜稽首曰。剌朕身。更朕先寶事。——盠方彝

在这则断为共王世的青铜器铭文中，我们可以看到，周天子命令盠管理六师和王行（天子私有军队）的三有司，也就是司工、司马、司土，一般认为，司工管理工程，司马管理军队，司土管理土地和人口，由此可知，六师、王行应该都是有其耕地的兵屯部队。

在西六师、殷八师的强大威力之下，天子不仅可以威慑周边戎狄，同样也可以震慑诸侯，让他们不敢造次。

在成康之际，周的扩张政策和分封制度让这个新生的国家不断兼并周边戎狄的土地，并促进了商人和周人的合作。

而到了昭王时期，一次失败的南征让天子的军队损失惨重：

周昭王十九年，天大曀，雉兔皆震，丧六师于汉。——竹书纪年

在这次军事行动返途中，浮桥垮塌，周昭王溺死，西六师受到巨大打击。这次军事失败让西周进入中期，其扩张速度明显减慢，开始从一个军事帝国向官僚制帝国转变，西周中期密集出现的册命金文正反映此时的政治面貌。

而西六师在上面盠方彝的例子中，应该也得到了重建。

值得注意的是，在西周中期，重要的军事行动主要中，已经出现了诸侯的军队辅助天子军队征伐的情况，在穆王世：

隹八月初吉。才宗周。甲戌。王令毛白更虢城公服。屏王立。乍四方亟。秉緐。蜀。巢。令易鈴勒。咸。王令毛公以邦冢君。土馭。【呈戈】人伐東国㾓戎。咸。王令吳白曰。以乃师左比毛父。王令呂白曰。以乃师右比毛父遣令曰厶乃族從父征。诞衛父身。——班簋

在班簋中，对东部方国的军事行动由毛公指挥，吴伯、吕伯协助，同时还有另一件青铜器可能说明这场战斗也有王师的参与：

众子鼓莓鑄旅簋。隹巢來迮。王令東宫。追以六师之年。

这件器铭中表明，对巢的军事行动是在太子（东宫）指挥下的六师完成的。

还有另一件青铜器说明在对东夷的战斗中，天子和地方诸侯的军队合作：

隹（唯）十又一月，王令（命）師俗、史密曰：“東征。”敆南尸（夷）膚虎會杞尸（夷）、舟尸（夷）雚不折，廣伐東或（國）齊（師）、族土、述（遂）人，乃執啚（鄙）寡亞。師俗（率）齊（師）、述（遂）人左，□伐長必，史密右，（率）族人、釐白（萊伯）、僰，周伐長必，隻（獲）百人，（敢揚）天子休，用乍（作朕）文考乙白（伯尊簋），子子孫孫（其）永寶——史密簋

在史密簋的铭文中，我们不难发现，在东征长必的军事行动中，由师俗和史密作为中央派出的军事长官，率领齐国、莱国等诸侯的军队进行征伐。

而到了西周晚期，由于多方面的原因，殷八师和西六师的战斗力大幅下降，变得软弱不堪：

呜呼哀哉！用天降大丧于下国，亦唯鄂侯驭方，率南淮夷、东夷广伐南国、东国，至于历内。王廼命西六、殷八，曰：“扑伐噩鄂侯驭方，勿遗寿幼。”肆师弥匌怵会恇，弗克伐鄂。肆武公廼遣禹率公戎车百乘、厮驭二百、徒千，曰：“于匡朕肃慕，唯西六、殷八伐噩鄂侯驭方，勿遗寿幼。”雩禹以武公徒驭至于鄂，敦伐鄂，休，获厥君驭方。肆禹有成。敢对扬武公不显耿光。用作大宝鼎。禹其万年子子孙宝用。——禹鼎

在厉王世对鄂侯驭方的灭国之战中，周天子押上西六师和殷八师全部力量，要消灭反叛的鄂国，却“弗克”，最终不得不依赖执政卿士武公的私人军队达成战略目的。

也就是在厉王世，高压专利的厉王被国人暴动赶出国家，参与暴动的大概也有王师的长官和军人，这个在我这篇回答中可以参考：周厉王时期国人暴动，周厉王为什么不调动军队镇压？

而到了宣王时，王师的战斗力有所恢复：

赫赫明明。王命卿士，南仲大祖，大师皇父。整我六师，以脩我戎。既敬既戒，惠此南国。
王谓尹氏，命程伯休父，左右陈行。戒我师旅，率彼淮浦，省此徐土。不留不处，三事就绪。
赫赫业业，有严天子。王舒保作，匪绍匪游。徐方绎骚，震惊徐方。如雷如霆，徐方震惊。
王奋厥武，如震如怒。进厥虎臣，阚如虓虎。铺敦淮濆，仍执丑虏。截彼淮浦，王师之所。
王旅啴啴，如飞如翰。如江如汉，如山之苞。如川之流，绵绵翼翼。不测不克，濯征徐国。
王犹允塞，徐方既来。徐方既同，天子之功。四方既平，徐方来庭。徐方不回，王曰还归。——诗经·常武

在大师皇父的指挥下，六师攻伐徐方（我祖宗，哼！），让徐方（我祖宗）臣服来宾。

可能在宣王世，由于对殷八师、西六师的掌控度下降，所以宣王又在宾服的南国建立了新的王师，但是这种尝试却未获成功，甚至成为了宣王中兴结束的诱因：

三十九年，战于千亩，王师败绩于姜氏之戎。宣王既亡南国之师，乃料民于太原。仲山甫谏曰：“民不可料也。”宣王不听，卒料民。——史记·周本纪

而在幽王末年的动乱中，西六师和殷八师并未见于史料，可能在这次战争中被消灭，或者不在天子的掌控范围之内了。

周幽王取妻于西申，生平王，王或（又）取褒人之女，是褒姒，生伯盤。褒姒嬖于王，王與伯盤逐平王，平王走西申。幽王起師，回（圍）平王于西申，申人弗畀。曾（繒）人乃降西戎，以攻幽王，幽王及伯盤乃滅，周乃亡。——清华简·系年（一）

所以显然，周天子的威严很大程度上来自于强大的西六师和殷八师，在这两支军队在战争中遭到损失或是天子对军队的掌控力下降之后，天子就无法再对诸侯建立起强大的控制。在西周末年，王师的衰落预示着西周秩序的崩溃。而在这之后的春秋时代里，某些显赫一时的诸侯也将会因为丧失对军队的掌控而消失在历史的尘埃之中。

因为姚雨平北伐，八千广东子弟过长江，把偏师打成了主力，整得清廷、清军、袁世凯、北洋军都懵逼了，连清廷死忠张勋都被揍得“赞同共和”……后世蒋介石、李济深、毛泽东、朱德、叶挺、林彪均以取名“第四军”为荣，源头就在姚雨平的北伐第四军。

姚雨平，毕业于广州黄埔陆军学堂，与黄兴、赵声一道策划了广州黄花岗起义，黄花岗起义时，黄兴、胡毅生、陈炯明、姚雨平四路进攻广州要地，但是因为偶然因素，黄兴已经失败了，姚雨平的队伍才拿到枪，不得已潜逃南洋。

辛亥革命时，姚雨平协助胡汉民力促广东光复，使广东成为辛亥革命中唯一一个完全由革命派控制军政大权的省份。其他各省份都或多或少的被立宪派、旧官僚渗透、控制，革命意志并不强烈，多倾向与清廷、袁世凯媾和，特别是“武昌首义”的湖北、第二起义的湖南，两省已然被立宪派、旧官僚操控，甚至策划遥尊袁世凯为大总统，加之汉口汉阳失陷，在革命阵营中，广东派上升、两湖帮下降。

而在当时的同盟会是由三大派组成的：

广东派，带头大哥孙中山，小弟胡汉民、许崇智、廖仲恺、朱执信

两湖派，大佬黄兴、宋教仁、谭人凤、孙武、陈其美（浙江人）

浙江派，大佬章炳麟、蔡元培、陶成章、朱瑞、李燮和（湖南人）

这三派互相争执，总的来说，由于黄兴既是两湖派带头大哥，又是孙中山的盟友，两湖派与广东派虽然时常发生矛盾，但不至于彻底撕破脸皮，而章炳麟、陶成章的光复会（浙江派）则同时和两湖派、广东派激烈冲突、已经彻底翻脸了。

这是一个大背景，为什么章炳麟多次“推举”黄兴、取代孙中山？为什么章炳麟在南京临时政府成立前“拥立”宋教仁当大总统？有些人非常单纯，以为章炳麟是真心的。。。章炳麟四处挑拨离间，结果就是他的手下陶成章死于非命。孙中山为什么在武昌起义爆发后迟迟不回国？原因也很简单，首义的湖北、湖南等地并不是他的地盘、也没有他的人马，他在等一个合适的时机。黄兴蹭蹭赶回去是必然的，因为两湖就是他地盘，所以轻而易举取得两湖军政大权，共进会文学社只得让位，黄兴在两湖革命党内地位过于崇高。

在武昌起义后，革命阵营中谁做大总统？宋教仁、黄兴都有可能，但是随着立宪派、旧官僚排挤革命党、掌握了两湖，他俩已经出局了，而孙中山的嫡系胡汉民掌握了广东全省军政大权，三次“倒孙”中备受打击的孙中山一下子走出了阴影。

1911 年 10 月 10 日，武昌起义

11 月 9 日，广东光复，孙中山嫡系人马胡汉民朱执信等控制广东一切军政，积极支援两湖、江浙革命，组织北伐军，胡汉民任命姚雨平为广东北伐军总司令，北伐军兵力 8000 人，年龄均在 30 岁以内，拥有炮兵营、机枪营，炮弹一万发，步枪子弹 300 万发，机枪子弹 50 万发，德制新式管退炮 18 尊。

12 月 2 日，广东北伐军先遣队参与江浙联军，南京光复。

12 月 19 日，广东北伐军主力到达上海

12 月 20 日，孙中山回国到广州，胡汉民、廖仲恺迎接

12 月 25 日，孙中山到上海，宋教仁、陈其美（被迫？）迎接欢迎，记者问孙中山：“你这次带多少钱来？”孙中山说：“予不名一钱也，所带回者革命之精神耳！”（你他娘还真幽默）

12 月 26 日，广东北伐军到达南京

1912 年 1 月 1 日，孙中山当选临时大总统

当时南北战局，以长江为划分来说，西线武昌“湖广总督”北洋段祺瑞与两湖革命军焦灼，中部安徽北洋倪嗣冲虎视眈眈，东部则是北洋悍将、“南洋大臣”兼署理“两江总督”的张勋威胁南京（此时张勋毫无疑问是北洋集团仅次于袁世凯的第二人，而他是忠心清廷的，其战斗力从后来二次革命“冯张争南京”来看，张勋军事能力要高于冯国璋）。

1912 年初，孙中山、黄兴发起六路伐清，姚雨平即为第四军总司令，林震为前敌总指挥，李济深、张文为参谋长，按最初计划，姚雨平北伐的目的只是捍卫南京、侧翼牵制倪嗣冲，结果创造了历史。

1912 年 1 月 18 日广东北伐军渡过长江，27 日，在固镇与张勋部队展开遭遇战，以死亡 40 人的代价、重创张勋部，俘虏一千人和缴获大量辎重弹药，占领固镇，同日得知此败报的段祺瑞等 46 名北洋将领通电要求清帝退位。29 日，张勋偷袭北伐军，被反杀，2 月 2 日双方再次激战，张勋溃退，2 月 4 日，双方在宿州展开决战，张勋部得北洋精锐第五镇 4000 人、山东 1000 清军、另有一营炮兵两营骑兵支援，与姚雨平激战 6 小时，张勋方面死伤一千人，被俘数百，再次败北，逃到徐州，不久发布声明“赞同共和”（说好的大清死忠辫子军张勋呢？），而后风闻姚雨平又至，惊慌失措，不久逃往山东济南，广东北伐军占领徐州，华北平原门户洞开。

2 月 12 日，清帝退位。（真鸡贼啊，趁着手里筹码没赔光就立即脱身了）

清帝退位后，姚雨平北伐军改名讨虏军，驻扎徐州、宿州一带，当此之时，袁世凯不愿南下就职大总统，指使属下在北京天津制造叛乱，谎称北方骚乱自己抽不开身，姚雨平通电北京称自己愿意率军进京平叛，袁世凯立即阻止，“此次之变，系少数游勇鼓动，叛者不过一标。。。勿劳大军北来”（姚雨平皮这一下很开心）

后来袁世凯当上大总统，对姚雨平进行拉拢，授予陆军中将加上将衔，姚雨平不为所动，不久姚雨平被削掉兵权，解散北伐军，二次革命失败后姚雨平继续追随孙中山。1922 年，孙中山遭陈炯明背叛、被困永丰舰，电报通传姚雨平，姚雨平从香港赶回来、随侍左右（后来蒋介石派系编写史书，整得好像孙中山只给蒋介石发电报求救、好像只有蒋介石到场护卫、好像蒋介石摆平陈炯明似的，事实上，孙中山被困永丰舰满世界发电报求救，姚雨平去的更早！也是在粤军中资历甚高的姚雨平帮忙摆平的）。

孙中山晚年联俄联共，许崇智等粤军不甚认可，姚雨平、张文等粤军元老表示支持，孙中山死后姚雨平心灰意冷、逐渐退出政坛，当然时不时也爱怼怼蒋介石，南昌起义后部队南下潮汕损失惨重，姚雨平“高抬贵手”放了起义军南下、后又率军舰欲接应起义部队。解放后，姚雨平从香港回到广州，曾为粤军参谋长的叶剑英亲自探望这个“粤军缔造者”、给予一闲差养老。文革时叶剑英力保，姚雨平并未受冲击，安然度过晚年。什么才是老革命啊！（战略后仰）

姚雨平北伐第四军——李济深国民革命军第四军（粤军）——毛泽东朱德工农红军第四军——叶挺项英新四军——林彪中国人民解放军第四野战军

国民大革命时，蒋在军队中排共，第一军中就把共产党都排挤了，而第四军，即粤军，粤系领袖是李济深，而他却是姚雨平一手提拔的，姚雨平资历太老了，李济深、张发奎都是小字辈，姚雨平却支持中共，所以粤军共产党多也就没啥奇怪了。南昌起义也主要是粤军中共产党搞得，后来朱毛井冈山会师，成立中国工农红军第四军，也是表明对原第四军的沿革。

相关阅读

宋教仁到底是谁刺杀的？为什么陶成章没有秋瑾和徐锡麟名气大？近代中国为什么只有革命一条道路可走？